Advertisements
Advertisements
प्रश्न
Evaluate: `int_-6^3 |x+3|dx`
उत्तर
`I = int_-6^3|x+3|dx`
`f(x)=|x+3|=X+3: X+3>0rArr X > -3`
= -x -3 ; x+3<0 ⇒ x < -3
`I = int_-6^3 |x+3| dx + int_-3^3(x+3)dx`
`I = -(x^2/2 +3x)_-6^-3 + (x^2/2+3x)_-3^3`
`I = - [(9/2 - 9)-(36/2 -18)]+[(9/2+9)-(9/2 - 9)]`
`I = -[-9/2]+18`
`I = 9/2 +18 = (9+36)/2 = 45/2`
Alternate method :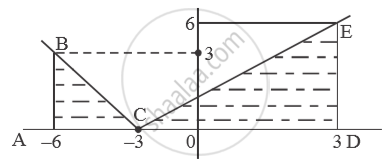
`int_-6^3 |x+3| dx `
= `A(DeltaABC)+A(DeltaCDE)`
`= 1/2xx3xx3+1/2xx6xx6`
`=9/2+18`
`=45/2`
APPEARS IN
संबंधित प्रश्न
Evaluate : `int(x1+x^2)/(1+x^4)dx`
Solve the differential equation `dy/dx = (x + y+2)/(2(x+y)-1)`
If A, B and C are the elements of Boolean algebra, simplify the expression (A’ + B’) (A + C’) + B’ (B + C). Draw the simplified circuit.
Prove that locus of z is circle and find its centre and radius if is purely imaginary.
For the set A = {1, 2, 3}, define a relation R in the set A as follows: R = {(1, 1), (2, 2), (3, 3), (1, 3)}. Write the ordered pairs to be added to R to make it the smallest equivalence relation.
Let f: R → R be the function defined by f(x) = `1/(2 - cosx)` ∀ x ∈ R.Then, find the range of f
If R is a relation from a non – empty set A to a non – empty set B, then ____________.
Let A = {a, b, c}, then the range of the relation R = {(a, b), (a, c), (b, c)} defined on A is ____________.
Number of relations that can be defined on the set A = {a, b, c, d} is ____________.
Let R be the relation in the set N given by R = {(a, b) : a = b – 2, b > 6}, then ______.
