Question

Explain in detail the Maxwell Boltzmann distribution function.

Answer 1

Maxwell-Boltzmann: In speed distribution function Consider an atmosphere, the air molecules are moving in random directions. The speed of each molecule is not the same even though macroscopic parameters like temperature and pressure are fixed. Each molecule collides with every other molecule and they exchange their speed. In previously we calculated the rms speed of each molecule and not the speed of each molecule which is rather difficult. In this scenario, we can find the number of gas molecules that move with the speed of 5 ms⁻¹ to 10 ms⁻¹ or 10 ms⁻¹ to 15 ms⁻¹ etc. In general, our interest is to find how many gas molecules have a range of speeds from v to v + dv. This is given by Maxwell’s speed distribution function.

N_v = `4π"N"("m"/2π"kT")^(3/2) "v"^2"e"^(-"mv"^2/(2"kT"))`

The above expression is graphically shown as follows:

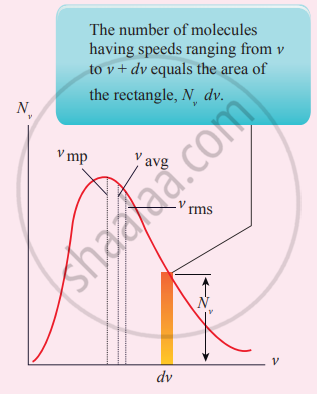
   Maxwell’s molecular speed distribution

From the above figure, it is clear that for a given temperature the number of molecules having lower speed increases parabolically but decreases exponentially after reaching the most probable speed. The ms speed, average speed and most probable speed are indicated in the figure. It can be seen that the rms speed is greatest among the three.

The figure shows the speed distribution graph for two different temperatures. As temperature increases, the peak of the curve is shifted to the right. It implies that the average speed of each molecule will increase. But the area under each graph is the same since it represents the total number of gas molecules.

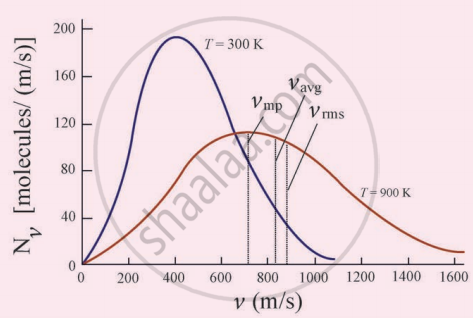
    Maxwell distribution graph for two different temperatures