Advertisements
Advertisements
प्रश्न
Find the least number of six digits which is a perfect square.
उत्तर
The least number with six digits is 100000. To find the least square number with six digits, we must find the smallest number that must be added to 100000 in order to make a perfect square. For that, we have to find the square root of 100000 by the long division method as follows:
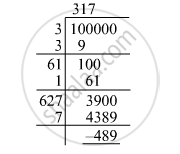
100000 is 489 (4389 − 3900) less than 3172. Hence, to be a perfect square, 489 should be added to 100000.
100000 + 489 = 100489
Hence, the least number of six digits that is a perfect square is 100489.
APPEARS IN
संबंधित प्रश्न
What will be the unit digit of the square of the given number?
3853
What will be the unit digit of the square of the given number?
52698
Find the least number which must be added to the following numbers to make them a perfect square:
5607
Find the least number which must be added to the following numbers to make them a perfect square:
37460
Find the square root of:
\[10\frac{151}{225}\]
Find the value of:
\[\frac{\sqrt{441}}{\sqrt{625}}\]
A number ending in 9 will have the units place of its square as ______.
A perfect square can never have the following digit in its ones place.
The square of 86 will have 6 at the units place.
Using distributive law, find the square of 101
