Advertisements
Advertisements
प्रश्न
Find the sum of all three digit natural numbers, which are multiples of 7 ?
उत्तर
Three digit natural numbers which are multiples of 7 are 105, 112, 119,…, 994.
105, 112, 119, … 994 are in A.P.
First term (a) = 105
Common difference (d) = 7
Let 994 be the nth term of A.P.
∴ an = 994
⇒ 105 + (n − 1) × 7 = 994 [ `therefore`an = a + (n − 1)d]
⇒ 7 (n − 1) = 994 − 105
⇒ 7 (n − 1) = 889
⇒ n − 1 = 127
⇒ n = 128
`\text{Sumof all terms of AP}=128/2(105+994)[thereforeS_n=n/2(a+l),\text{being last term}]`
`=64xx1099`
`=70336`
Thus, the sum of all three digit natural numbers which are multiples of 7 is 70336.
APPEARS IN
संबंधित प्रश्न
Find the sum of the following.
`(1 - 1/n) +(1 -2/n) + (1- 3/n) +` ......up to n terms.
The sum first 10 terms of an AP is -150 and the sum of its next 10 terms is -550 . Find the AP.
The sum of the first 7 terms of an A.P. is 63 and the sum of its next 7 terms is 161. Find the 28th term of this A.P ?
Find the number of terms of the AP − 12, −9, −6, ….., 12. If 1 is added to each term of this AP, then find the sum of all terms of the AP thus obtained ?
Write the correct number in the given boxes from the following A. P.
3, 6, 9, 12,...
Here t1 =  t2 =
t2 =  , t3 =
, t3 =  , t4 =
, t4 =  ,
,
t2 – t1 =  , t3 – t2 =
, t3 – t2 =  ∴ d =
∴ d = 
Observe the adjacent Venn diagram and write the complement of A.
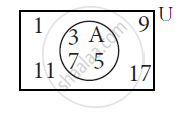
A = {1, 2, 3,4, 5}, B = {5, 6, 7} write AUB .
Find the eighteenth term of the A.P: 1, 7, 13, 19, ............
Find S2 for the A.P. 3,5,7,9,......
Find the value of the determinate:
`|(4,-2),(3,1)|`
