Advertisements
Advertisements
प्रश्न
Find the area of the region bounded by the parabola y2 = 25x and the line x = 5.
उत्तर
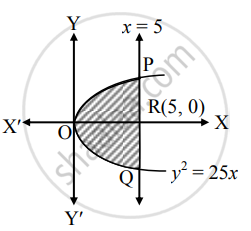
The given equation of the parabola is y2 = 25x
∴ y = `5sqrt(x)` ...[∵ In the first quadrant, y > 0]
Required area = area of the region OQRPO
= 2 (area of the region ORPO)
= `2 int_0^5 y*dx`
= `2 int_0^5 5sqrt(x)*dx`
= `10 int_0^5 x^(1/2)*dx`
= `10[x^(3/2)/(3/2)]_0^5`
= `(20)/(3)[(5)^(3/2) - 0]`
= `(20)/(3) (5sqrt((5))`
= `(100sqrt(5))/(3)` sq. units.
संबंधित प्रश्न
Find the area of circle x2 + y2 = 25.
Solve the following :
Find the area between the parabolas y2 = 7x and x2 = 7y.
State whether the following statement is True or False:
y2 = 4ax is the standard form of parabola when curve lies on X-axis
State whether the following statement is True or False:
Standard form of parabola is x2 = – 4by, when curve lies in the positive Y-axis
Find the area between the parabolas y2 = 5x and x2 = 5y
