Question

Find the equivalent capacitance between P and Q in the following diagram. The area of each plate is A and the separation between plates is d.

Answer 1

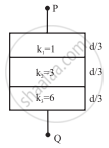
(i) The capacitor in the first diagram is a series combination of three capacitors of plate separations d/3 and plate areas A, with C₁ filled with air (k₁= 1), C₂ filled with a dielectric of k₂ = 3, and C₃ filled with a dielectric of k₃ = 6.

∴ `"C"_1 = ("k"_1ε_0"A")/("d"//3) = (3ε_0"A")/"d" "k"_1, "C"_2 = ("k"_2ε_0"A")/("d"//3) = (3ε_0"A")/"d" "k"_2`,

`"C"_3 = ("k"_3ε_0"A")/("d"//3) = (3ε_0"A")/"d" "k"_3`

∴ `1/"C'" = 1/"C"_1 + 1/"C"_2 + 1/"C"_3 = "d"/(3ε_0"A")(1/"k"_1 + 1/"k"_2 + 1/"k"_3)`

∴ C' = `(3ε_0"A")/"d"(("k"_1"k"_2"k"_3)/("k"_1"k"_2 + "k"_2"k"_3 + "k"_3"k"_1)) = (3ε_0"A")/"d" (18/27)`

= `(2ε_0"A")/"d"`

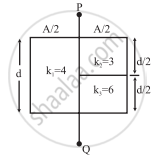
(ii) A series combination of two capacitors  C₂ (k₂ = 3) and C₃ (k₃ = 6) of plate areas A/2 and plate separations d/2 is in parallel with a capactor C₁ (k₁ = 4) of plate area A/2 and plate separation d in the second figure above.

∴ `"C"_1 = ("k"_1ε_0("A"//2))/"d" = (ε_0"A")/"2d" "k"_1`

`"C"_2 = ("k"_2ε_0("A"//2))/("d"//2) = (ε_0"A")/"d" "k"_2`

`"C"_3 = ("k"_3ε_0("A"//2))/("d"//2) = (ε_0"A")/"d" "k"_3`

∴ For the series combination of C₂ and C₃,

`1/"C"_4 = 1/"C"_2 + 1/"C"_3`

∴ `"C"_4 = ("C"_2"C"_3)/("C"_2 + "C"_3) = (ε_0"A")/"d"(("k"_2"k"_3)/("k"_2 + "k"_3)) = (ε_0"A")/"d" ((3xx6)/(3+6)) = (2ε_0"A")/"d"`

Finally, for the parallel combination of C₁ and C₄, 

C'' = `"C"_1 + "C"_4 = (ε_0"A")/"2d" (4) + (2ε_0"A")/"d" = (4ε_0"A")/"d"`

Thus, the equivalent capacitances are C' = `(2ε_0"A")/"d"` and C'' = `(4ε_0"A")/"d"`.