Advertisements
Advertisements
प्रश्न
Find the value of x so that `(5/3)^-2 xx (5/3)^-14 = (5/3)^(8x)`
उत्तर
We have, `(5/3)^-2 xx (5/3)^-14 = (5/3)^(8x)`
Using law of exponents, am × an = (a)m + n ...[∵ a is non-zero integer]
Then, `(5/3)^-2 xx (5/3)^-14 = (5/3)^(8x)`
⇒ `(5/3)^(-2 - 14) = (5/3)^(8x)`
⇒ `(5/3)^(-16) = (5/3)^(8x)`
On comparing both sides, we get
16 = 8x
⇒ x = – 2
APPEARS IN
संबंधित प्रश्न
3–2 can be written as ______.
If x be any non-zero integer and m, n be negative integers, then xm × xn is equal to ______.
The value of (7–1 – 8–1) –1 – (3–1 – 4–1) –1 is ______.
`(1/10)^0` is equal to ______.
a3 × a–10 = ______.
The value of [2–1 × 3–1]–1 is ______.
Use the properties of exponents to verify that statement is true.
`4^(n - 1) = 1/4(4)^n`
Find a single repeater machine that will do the same work as hook-up.
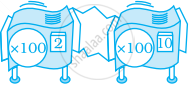
For hook-up, determine whether there is a single repeater machine that will do the same work. If so, describe or draw it.
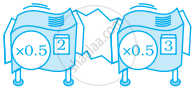
By what number should (–8)–3 be multiplied so that the product may be equal to (–6)–3?
