Advertisements
Advertisements
प्रश्न
For a particle performing uniform circular motion, choose the correct statement(s) from the following:
- Magnitude of particle velocity (speed) remains constant.
- Particle velocity remains directed perpendicular to radius vector.
- Direction of acceleration keeps changing as particle moves.
- Angular momentum is constant in magnitude but direction keeps changing.
उत्तर
a, b and c
Explanation:
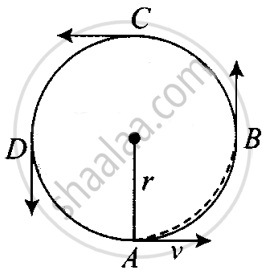
For a particle performing uniform circular motion.
- Speed will be constant throughout.
- Velocity will be tangential in the direction of motion at a particular point.
- Acceleration `a = v^2/r` will always be towards centre of the circular path.
- Angular momentum (mvr) is constant in magnitude and direction/out of the plane perpendicularly as well.
APPEARS IN
संबंधित प्रश्न
A particle rotates in U.C.M. with tangential velocity V along a horizontal circle of diameter ‘D' . Total angular displacement of the particle in time 't' is..........
Read the statement below carefully and state, with reason, if it is true or false:
The velocity vector of a particle at a point is always along the tangent to the path of the particle at that point.
Is it possible to have an accelerated motion with a constant speed? Explain
Earth moves around the sun with uniform velocity.
Which of the following quantity remains constant in a uniform circular motion?
Solve the following problem.
A car moves in a circle at a constant speed of 50 m/s and completes one revolution in 40 s. Determine the magnitude of the acceleration of the car.
Statement A: Uniform circular motion is a case of accelerated motion
Statement B: In the third equation of motion we do not have the term time
A point object moves along an arc of a circle of radius 'R'. Its velocity depends upon the distance covered 'S' as V = `Ksqrt(S)` where 'K' is a constant. If 'e' is the angle between the total acceleration and tangential acceleration, then
A rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a massless string tied to point Q as shown in figure. When string is cut, the initial angular acceleration of the rod is ______.
A particle moves along a circle of radius r with constant tangential acceleration. If the velocity of the particle is v at the end of second revolution, after the revolution has started, then the tangential acceleration is ______.
