Advertisements
Advertisements
प्रश्न
Form the quadratic equation from the roots given below.
3 and –10
उत्तर
3 and –10
Sum of roots = 3 + (–10) = −7
Product of roots = 3 \[\times\]–10 = –30
The general form of the quadratic equation is \[x^2 - \left( \text{ Sum of roots } \right)x + \text{ Product of roots } = 0\]
So, the quadratic equation obtained is \[x^2 - \left( - 7 \right)x + \left( - 30 \right) = 0\]
\[x^2 + 7x - 30 = 0\]
APPEARS IN
संबंधित प्रश्न
Find the root of the following equation.
`1/(x+4) - 1/(x-7) = 11/30, x ≠ -4, 7`
The difference of squares of two numbers is 180. The square of the smaller number is 8 times the larger number. Find the two numbers
Two water taps together can fill a tank in `9 3/8`hours. The tap of larger diameter takes 10 hours less than the smaller one to fill the tank separately. Find the time in which each tap can separately fill the tank.
Find the roots of the following quadratic equations (if they exist) by the method of completing the square.
3x2 + 11x + 10 = 0
Find the roots of the following quadratic equations (if they exist) by the method of completing the square.
`sqrt2x^2-3x-2sqrt2=0`
`2/x^2-5/x+2=0`
`sqrt2x^3-3x-2sqrt2=0`
The area of a right triangle is `600cm^2` . If the base of the triangle exceeds the altitude by 10 cm, find the dimensions of the triangle.
The area of right-angled triangle is 96 sq meters. If the base is three time the altitude, find the base.
Solve the following quadratic equation by completing the square method.
5x2 = 4x + 7
Fill in the gaps and complete.
If α, β are roots of quadratic equation,
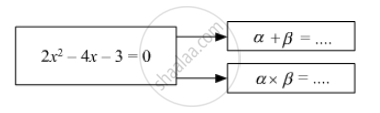
Find the value of discriminant.
x2 + 7x – 1 = 0
Find the value of discriminant.
2y2 – 5y + 10 = 0
Determine the nature of roots of the following quadratic equation.
x2 – 4x + 4 = 0
Form the quadratic equation from the roots given below.
\[\frac{1}{2}, - \frac{1}{2}\]
α, β are roots of y2 – 2y –7 = 0 find,
α3 + β3
The sum of the squares of two consecutive multiples of 7 is 637. Find the multiples.
The sum of the squares of two consecutive even numbers is 340. Find the numbers.
The value of `sqrt(6 + sqrt(6 + sqrt(6 ....)))`
If p2x2 – q2 = 0, then x =?
