Question

Form the point of intersection (P) of lines given by x₂ – y² – 2x + 2y = 0, points A, B, C, Dare taken on the lines at a distance of `2sqrt(2)` units to form a quadrilateral whose area is A₁ and the area of the quadrilateral formed by joining the circumcentres of ΔPAB, ΔPBC, ΔPCD, ΔPDA is A₂, then `A_1/A_2` equals

पर्याय

• 2

• 4

• `sqrt(3)`

• 1

Answer 1

2

Explanation:

x₂ – y² – 2x + 2y = 0 gives y = x and x + y = 2

Points A and C can be calculated using parametric form, `x = 1 +- 2sqrt(2) cos 45, y = 1 +- 2sqrt(2) sin 45  A(3, 3), C(-1, - 1)`

Similarly, for B and D,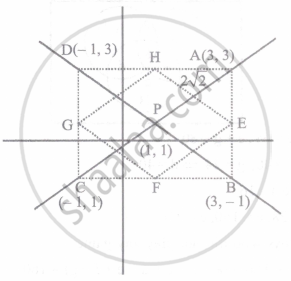

`x = 1 +- 2sqrt(2) cos  (3pi)/4, y = 1 +- 2sqrt(2) sin  (3pi)/4`

So, B = (3, –1), D = (–1, 3)

So A₁ = 4 × 4 = 16

Now, As ΔPAB, ΔPBC, ΔPCD and ΔPDA are right-angle triangles, so their circumcentres are the mid-point of AB, BC, CD and DA.

i.e., E(3, 1), F(1, –1), G(–1, 1) , H(1, 3) which again form a square whose area A₂ = `(2sqrt(2))^2` = 8

∴ `A_1/A_2 = 16/8` = 2