Advertisements
Advertisements
प्रश्न
From a point P on the ground the angle of elevation of the top of a tower is 30° and that of the top of a flag staff fixed on the top of the tower, is 60°. If the length of the flag staff is 5 m, find the height of the tower.
उत्तर
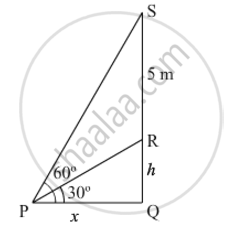
Let RQ be the tower and SR be the flag staff.
In ∆PQR,
`tan30^@=(RQ)/(PQ)`
`=>1/sqrt3=h/x`
`=>x=hsqrt3 " .....(i)"`
In ∆PQS
`tan 60^@=(SQ)/(PQ)`
`=>sqrt3=(h+5)/x`
`=>xsqrt()3=h+5" .....(ii)"`
From (i) and (ii), we get
3h=h+5
⇒2h=5
⇒h=2.5 m
Hence, the height of the tower is 2.5 metres.
APPEARS IN
संबंधित प्रश्न
A passenger, while boarding the plane, slipped form the stairs and got hurt. The pilot took the passenger in the emergency clinic at the airport for treatment. Due to this, the plane got delayed by half an hour. To reach the destination 1500 km away in time, so that the passengers could catch the connecting flight, the speed of the plane was increased by 250 km/hour than the usual speed. Find the usual speed of the plane
What value is depicted in this question?
The angles of elevation of the top of a rock from the top and foot of a 100 m high tower are respectively 30° and 45°. Find the height of the rock.
Two poles of equal heights are standing opposite to each other on either side of the road which is 80m wide, From a point P between them on the road, the angle of elevation of the top of one pole is 60 and the angle of depression from the top of another pole at P is 30 . Find the height of each pole and distance of the point P from the poles.
The angle of elevation on the top of a building from the foot of a tower is 30° . The angle of elevation of the top of the tower when seen from the top of the second water is 60° .If the tower is 60m high, find the height of the building.
A bucket is in the form of a frustum of a cone and it can hold 28.49 litres of water. If the radii of its circular ends are 28 cm and 21 cm, find the height of the bucket. [Use`pi22/7` ]
A person is standing at a distance of 80 m from a church looking at its top. The angle of elevation is of 45°. Find the height of the church.
A boy standing at a distance of 48 meters from a building observes the top of the building and makes an angle of elevation of 30°. Find the height of the building.
When the length of shadow of a vertical pole is equal to `sqrt3` times its height, the angle of elevation of the Sun’s altitude is ____________.
In the given figure, AB is tower of height 50 m. A man standing on its top, observes two car on the opposite sides of the tower with angles of depression 30° and 45° respectively. Find the distance between the two cars.

From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 30°. Determine the height of the tower.
