Advertisements
Advertisements
प्रश्न
Given that the number \[\overline{{35\alpha64}}\] is divisible by 3, where α is a digit, what are the possible values of α?
उत्तर
\[\text{ It is given that } \overline{{35a64}} \text{ is a multiple of 3 }. \]
\[ \therefore (3 + 5 + a + 6 + 4) \text{ is a multiple of 3 }. \]
\[ \therefore (a + 18)\text{ is a multiple of 3} . \]
\[ \therefore (a + 18) = 0, 3, 6, 9, 12, 15, 18, 21 . . . \]
\[\text{ But a is a digit of number }\overline{{35a64}} \text{. So, a can take value }0, 1, 2, 3, 4 . . . 9 . \]
\[a + 18 = 18 \Rightarrow a = 0\]
\[a + 18 = 21 \Rightarrow a = 3\]
\[a + 18 = 24 \Rightarrow a = 6\]
\[a + 18 = 27 \Rightarrow a = 9\]
\[ \therefore a = 0, 3, 6, 9\]
APPEARS IN
संबंधित प्रश्न
1×5 divisible by 3?
31×5 divisible by 3?
There are some flowering trees in a garden. Each tree bears many flowers with the same number printed on it. Three children took a basket each to pick flowers. Each basket has one of the numbers, 3, 4 or 9 on it. Each child picks those flowers which have numbers divisible by the number on his or her basket. He/She takes only 1 flower from each tree. Can you tell which numbers the flowers in each basket will have?
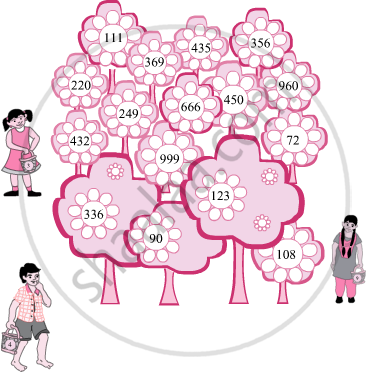
Check the divisibility of 2146587 by 3.
Check the divisibility of 15287 by 3.
Find the dates of any month in a calendar which are divisible by both 2 and 3.
The least number that should be added to 57 so that the sum is exactly divisible by 2, 3, 4 and 5 is __________
If the sum of digits of a number is divisible by three, then the number is always divisible by ______.
3134673 is divisible by 3 and ______.
Number of the form 3N + 2 will leave remainder 2 when divided by 3.
