Advertisements
Advertisements
प्रश्न
How is the magnetic field of a small current loop identical to that of a short magnetic dipole? Explain.
स्पष्ट करा
उत्तर
- An electric current in a circular loop establishes a magnetic field similar in every respect to the field of a magnetic dipole (or a bar magnet).
- Consider a circular conducting loop of radius R, axis along the X-axis and carrying a current I.
- The area of the loop is A= πR2 and `vecA` has the direction given by right hand rule. The axial magnetic induction of the current loop at a distance x from its centre is `vecB =(mu_0/(4pi))(2IvecA)/(R^2+x^2)^(3/2)`
`vecB =(mu_0/(4pi))(2vecM)/(R^2+x^2)^(3/2)` - where `vecM = IvecA` is the magnetic moment of the current loop and µ0 is the permeability of free space.
- For x > > R, ignoring R2 in comparison with x2 `B = (mu_0/(4pi)) (2 vecM)/x^3`
- This equation also gives the magnetic induction on the axis of a short magnetic dipole (or a bar magnet) of magnetic moment `vecM`.
- For a magnetic dipole, the dipole moment is directed from the south pole of the dipole to its north pole. For a current loop, the mangetic dipole moment has the direction of the axial field of the current loop as given by the right hand rule.

- When an observer looking at a current carrying circular loop finds the direction of the current anticlockwise, the face of the loop towards the observer acts as the north pole.
- When an observer looking at a current carrying circular loop finds the direction of the current clockwise, the face of the loop towards the observer acts as the south pole. This rule is known as the clock rule.
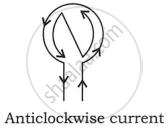
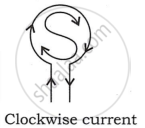
shaalaa.com
Magnetic Lines for a Current Loop
या प्रश्नात किंवा उत्तरात काही त्रुटी आहे का?
