Advertisements
Advertisements
प्रश्न
How many tiles whose length and breadth are 12 cm and 5 cm respectively will be needed to fit in a rectangular region whose length and breadth are:
100 cm and 144 cm
उत्तर
Area of rectangle = 100 × 144
= 14400 cm
Area of one tile = 5 × 12
= 60 cm2
Number of tiles = `"(Area of rectangle)"/"(Area of one tile)"`
= `14400/60`
= 240
Hence, 240 tiles are needed.
APPEARS IN
संबंधित प्रश्न
A rectangular hall is 12 m long and 6 m broad. Its flooring is to be made of square tiles of side 30 cm. How many tiles will fit in the entire hall? How many would be required if tiles of side 15 cm were used?
What will be the labour cost of laying the floor of an assembly hall that is 16 m long and 12 m wide if the cost of laying 1 sq m is 80 rupees?
Find the area of the rectangle whose sides are:
12 m and 21 m
Find the area of the rectangle whose sides are:
2 km and 3 km
What is the cost of tiling a rectangular plot of land 500 m long and 200 m wide at the rate of ₹ 8 per hundred sq m.?
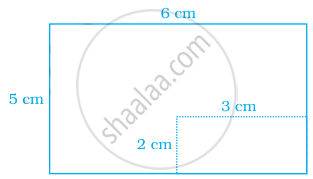
A rectangular piece of dimensions 3 cm × 2 cm was cut from a rectangular sheet of paper of dimensions 6 cm × 5 cm (see the figure). Area of remaining sheet of paper is ______.
A carpet of size 5 m × 2 m has 25 cm wide red border. The inner part of the carpet is blue in colour (see the figure). Find the area of blue portion. What is the ratio of areas of red portion to blue portion?

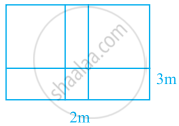
A school playground is divided by a 2 m wide path which is parallel to the width of the playground, and a 3 m wide path which is parallel to the length of the ground in the given figure. If the length and width of the playground are 120 m and 80 m respectively, find the area of the remaining playground.
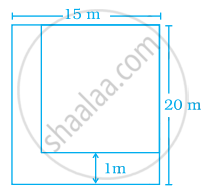
In a park of dimensions 20 m × 15 m, there is a L shaped 1 m wide flower bed as shown in the figure. Find the total cost of manuring for the flower bed at the rate of Rs 45 per m2.
4 squares each of side 10 cm have been cut from each corner of a rectangular sheet of paper of size 100 cm × 80 cm. From the remaining piece of paper, an isosceles right triangle is removed whose equal sides are each of 10 cm length. Find the area of the remaining part of the paper.
