Advertisements
Advertisements
प्रश्न
If a LC circuit is considered analogous to a harmonically oscillating spring block system, which energy of the LC circuit would be analogous to potential energy and which one analogous to kinetic energy?
उत्तर
When a charged capacitor C having an initial charge q0 is discharged through an inductance L, the charge and current in the circuit starts oscillating simple harmonically. If the resistance of the circuit is zero, no energy is dissipated as heat. We also assume an idealized situation in which energy is not radiated away from the circuit. The total energy associated with the circuit is constant.
The oscillation of the LC circuit is electromagnetic analogous to the mechanical oscillation of a block-spring system.
The total energy of the system remains conserved.
`1/2 CV^2 + 1/2 LI^2` = constant = `1/2 CV_0^2 = 1/2 LI^2`
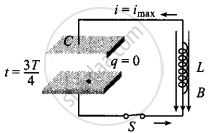
At t = `(3T)/4`, capacitor again discharges completely i = imax
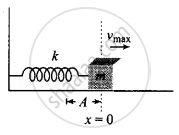
At `t = (T)/2`, block again reaches its mean position and its velocity becomes maximum
Comparison of oscillation of a mass-spring system and an LC circuit
| Mass spring system | v/s | LC circuit |
| Displacement `(x)` | Charge `(q)` | |
| Velocity `(v)` | Current `(i)` | |
| Acceleration `(a)` | Rate of change of current `((di)/(dt))` | |
| Mass `(m)` [Inertia] | Inductance `(L)` [Inertia of electricity] | |
| Momentum `(p = mv)` | Magnetic flux `(phi = Li)` | |
| Retarding force `(-m (dv)/(dt))` | Self induced emf `(-L (di)/(dt))` |
|
Equation of free oscillations: `(d^2x)/(dt^2) = - ω^2x`; where ω = `sqrt(K/m)` |
Equation of free oscillations: `(d^2q)/(dt^2) = - (1/(LC)).q`; where ω2 = `1/(LC)` |
|
| Force constant K | Capacitance C | |
| Kinetic energy = `1/2 mv^2` | Magnetic energy = `1/2 Li^2` | |
| Elastic potential energy = `1/2 Kx^2` | Electrical potential energy = `1/2 q^2/C` |
If we consider an L-C circuit analogous to a harmonically oscillating spring block system. The electrostatic energy `1/2 CV^2` is analogous to potential energy and energy associated with moving charges (current) that is magnetic energy `(1/2 LI^2)` is analogous to kinetic energy.
APPEARS IN
संबंधित प्रश्न
Discuss the composition of two S.H.M.s along the same path having same period. Find the resultant amplitude and intial phase.
Answer in brief.
The total impedance of a circuit decreases when a capacitor is added in series with L and R. Explain why?
A charged 10 microfarad capacitor is connected to an 81 mH inductor. What is the angular frequency of free oscillations of the circuit?
A radio can tune over the frequency range of a portion of the MW broadcast band (800kHz -1200kHz). If its LC circuit has an effective inductance of 200mH, what must be the range of its variable condenser?
Electrical oscillations of desired frequency can be obtained by ______.
The magnetic field energy in an inductor changes from maximum value to minimum value in 10 ms, when connected to an a.c. source. The frequency of the source is ______.
In an oscillating LC circuit, the maximum charge on the capacitor is Q. The charge on the capacitor, when the energy is stored equally between the electric and magnetic field is ____________.
A charged 30 µF capacitor is connected to a 27 mH inductor. What is the angular frequency of free oscillations of the circuit?
An LC circuit contains a 20 mH inductor and a 50 µF capacitor with an initial charge of 10 mC. The resistance of the circuit is negligible. Let the instant the circuit is closed be t = 0.
(a) What is the total energy stored initially? Is it conserved during LC oscillations?
(b) What is the natural frequency of the circuit?
(c) At what time is the energy stored
(i) completely electrical (i.e., stored in the capacitor)?
(ii) completely magnetic (i.e., stored in the inductor)?
(d) At what times is the total energy shared equally between the inductor and the capacitor?
(e) If a resistor is inserted in the circuit, how much energy is eventually dissipated as heat?
When a charged condenser is allowed to discharge through the inductor the electrical oscillations are produced called ______
