Question

If both the roots of the quadratic equation x² – 2kx + k² + k – 5 = 0 are less than 5, then k lies in the interval is ______.

पर्याय

• (5, 6]

• (6, ∞)

• (–∞, 4)

• [4, 5]

Answer 1

If both the roots of the quadratic equation x² – 2kx + k² + k – 5 = 0 are less than 5, then k lies in the interval is (–∞, 4).

Explanation:

Given that both roots of quadratic equation are less than 5 then

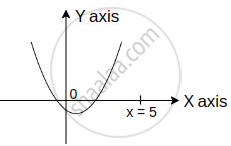
(i) Discriminant ≥ 0

4k² – 4(k² + k – 5) ≥ 0

⇒ 4k² – 4k² – 4k + 20 ≥ 0

⇒ 4k ≤ 20

⇒ k ≤ 5

(ii) p(5) > 0

⇒ f(5) > 0 ; 25 – 10k + k² + k – 5 > 0

⇒ k² – 9k + 20 > 0

⇒ k(k – 4) – 5(k – 4) > 0

⇒ (k – 5) (k – 4) > 0

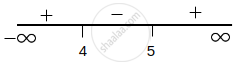
⇒ k ∈ (–∞, 4) ∪ (5, ∞)

(iii) `"Sum of roots"/2 < 5`

⇒ `-b/(2a) = (2k)/2 < 5`

⇒ k < 5

The intersection of (i), (ii) and (iii) gives k ∈ (–∞, 4).