Question

If f(x) = `x + 1/x, x ne 0`, then local maximum and x minimum values of function f are respectively.

पर्याय

• - 1 and 1

• - 2 and 2

• 2 and - 2

• 1 and - 1

Answer 1

- 2 and 2

Explanation:

We have, f(x) = `x + 1/x, x ne 0`

On differentiating w.r.t. x, we get

f'(x) = `1 - 1/x^2` and f''(x)

For maxima or minima, we put f'(x) = 0

`=> 1 - 1/x^2` = 0

⇒ x² - 1 = 0

⇒ x = -1, 1

Now, since f'(x) > 0, x ∈ (-1 - h, - 1) and

f'(x) < 0, x ∈ (-1, -1 + h)

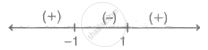
⇒ x = - 1 is point of local maxima.

and local maxima value is f(-1) = `- 1 + 1/(- 1) = - 2`

and f'(x) < 0, when x ∈ (1- h, 1)

and f"(x) > 0, when x ∈ (1, 1+ h)

⇒ x = 1 is point of minima.

and local minima value, f(1) = `1 + 1/1 = 2`