Advertisements
Advertisements
प्रश्न
If n(A ∪ B ∪ C) = 100, n(A) = 4x, n(B) = 6x, n(C) = 5x, n(A ∩ B) = 20, n(B ∩ C) = 15, n(A ∩ C) = 25 and n(A ∩ B ∩ C) = 10, then the value of x is
पर्याय
10
15
25
30
उत्तर
15
Explanation;
Hint:
n(A ∪ B ∪ C) = n(A) + n(B) + n(C) – n(A ∩ B) – n(B ∩ C) – n(A ∩ C) + n(A ∩ B ∩ C)
100 = 4x + 6x + 5x – 20 – 15 – 25 + 10
100 = 15x – 50
⇒ 150 = 15x
⇒ x = `150/15`
= 10
APPEARS IN
संबंधित प्रश्न
Given:
A = {Natural numbers less than 10}
B = {Letters of the word ‘PUPPET’}
C = {Squares of first four whole numbers}
D = {Odd numbers divisible by 2}.
Find: n(D)
Given:
A = {Natural numbers less than 10}
B = {Letters of the word ‘PUPPET’}
C = {Squares of first four whole numbers}
D = {Odd numbers divisible by 2}.
Find: n(B ∪ D)
Given:
A = {Natural numbers less than 10}
B = {Letters of the word ‘PUPPET’}
C = {Squares of first four whole numbers}
D = {Odd numbers divisible by 2}.
Find: n(B ∪ C)
Given:
A = {Natural numbers less than 10}
B = {Letters of the word ‘PUPPET’}
C = {Squares of first four whole numbers}
D = {Odd numbers divisible by 2}.
Find: n(A ∪ D)
If U = {x : x ∈ N, x ≤ 10}, A = {2, 3, 4, 8, 10} and B = {1, 2, 5, 8, 10}, then verify that n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
In a party of 45 people, each one likes tea or coffee or both. 35 people like tea and 20 people like coffee. Find the number of people who do not like tea
In the adjacent diagram, if n(U) = 125, y is two times of x and z is 10 more than x, then find the value of x, y and z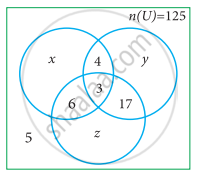
Each student in a class of 35 plays atleast one game among chess, carrom and table tennis. 22 play chess, 21 play carrom, 15 play table tennis, 10 play chess and table tennis, 8 play carrom and table tennis and 6 play all the three games. Find the number of students who play chess and carrom but not table tennis (Hint: Use Venn diagram)
If J = Set of three sided shapes, K = Set of shapes with two equal sides and L = Set of shapes with right angle, then J ∩ K ∩ L is
In a city, 40% people like only one fruit, 35% people like only two fruits, 20% people like all the three fruits. How many percentage of people do not like any one of the above three fruits?
