Advertisements
Advertisements
प्रश्न
If p : He swims
q : Water is warm
Give the verbal statement for the following symbolic statement.
q → p
उत्तर
If water is warm then he swims.
APPEARS IN
संबंधित प्रश्न
Using truth table prove that p ↔ q = (p ∧ q) ∨ (~p ∧ ~q).
Write the following compound statement symbolically.
Angle is neither acute nor obtuse.
Write the following compound statement symbolically.
If Δ ABC is right-angled at B, then m∠A + m∠C = 90°
Write the following compound statement symbolically.
x is not irrational number but is a square of an integer.
Construct the truth table of the following:
∼ (∼p ∧ ∼q) ∨ q
Express the following statement in symbolic form.
Milk is white or grass is green.
Write the negation of the following statement.
− 3 is a natural number.
Write the negation of the following statement.
It is false that Nagpur is capital of Maharashtra
Find the truth value of the following statement.
Neither 27 is a prime number nor divisible by 4.
If p and q are true and r and s are false, find the truth value of the following compound statement.
~ [p ∨ (r ∧ s)] ∧ ~ [(r ∧ ~ s) ∧ q]
If p : He swims
q : Water is warm
Give the verbal statement for the following symbolic statement.
p ↔ ~ q
Fill in the blanks :
Conjunction of two statement p and q is symbolically written as ______.
Fill in the blanks :
Negation of “some men are animal” is –––––––––.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
The Sun has set and Moon has risen.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
3 is prime number if 3 is perfect square number.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
Kavita is brilliant and brave.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
If Kiran drives the car, then Sameer will walk.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
It is not true that intelligent persons are neither polite nor helpful.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
If the question paper is not easy then we shall not pass.
If p : Proof is lengthy.
q : It is interesting.
Express the following statement in symbolic form.
It is not true that the proof is lengthy but it is interesting.
If p : Proof is lengthy.
q : It is interesting.
Express the following statement in symbolic form.
It is interesting iff the proof is lengthy.
Let p : Sachin wins the match.
q : Sachin is a member of Rajya Sabha.
r : Sachin is happy.
Write the verbal statement of the following.
(p ∧ q) ∨ r
Let p : Sachin wins the match.
q : Sachin is a member of Rajya Sabha.
r : Sachin is happy.
Write the verbal statement of the following.
p→(q ∨ r)
Rewrite the following statement without using the connective ‘If ... then’.
If it rains then the principal declares a holiday.
Negation of p → (p ˅ ∼ q) is ______
Without using truth table show that -
(p ˅ q) ˄ (∼p v ∼q) ≡ (p ∧ ∼q) ˄ (∼p ∧ q)
Negation of “Some men are animal “ is ______
Write the negation of the statement “An angle is a right angle if and only if it is of measure 90°”
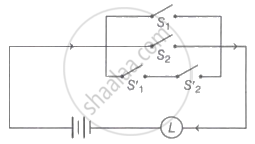
The symbolic form of the following circuit is (where p, q represents switches S1 and S2 closed respectively)
The negation of (p ∨ ∼q) ∧ q is ______
Which of the following is NOT true for p → q.
The Boolean expression ∼(q ⇒ ∼p) is equivalent to: ______
Let S be a non-empty subset of R. Consider the following statement:
p: There is a rational number x ∈ S such that x > 0. Which of the following statements is the negation of the statement p?
Write the converse, inverse, and contrapositive of the statement. "If 2 + 5 = 10, then 4 + 10 = 20."
Write the following statement in symbolic form.
It is not true that `sqrt(2)` is a rational number.
Express the following compound statement symbolically:
Delhi is in India but Dhaka is not in Sri Lanka
Write the contrapositive of the inverse of the statement:
‘If two numbers are not equal, then their squares are not equal’.
