Advertisements
Advertisements
प्रश्न
If the point P(2, 2) is equidistant from the points A(−2, k) and B(−2k, −3), find k. Also find the length of AP.
उत्तर
The given points are P(2, 2), A(−2, k) and B(−2k, −3).
We know that the distance between the points,(x1,y1) and (x2,y2)is given by:
`d=sqrt((x_2-x_1)^2+(y_2-y_1)^2)`
It is given that P is equidistant from A and B.
∴ AP = BP
⇒ AP2 = BP2
⇒ (2 − (−2))2 + (2 − k)2 = (2 − (−2k))2 + (2 − (−3))2
⇒ (4)2 + (2 − k)2 = (2 + 2k)2 + (5)2
⇒ 16 + k2 + 4 − 4k = 4 + 4k2 + 8k + 25
⇒ 3k2 + 12k + 9 = 0
⇒ k2 + 4k + 3 = 0
⇒ k2 + 3k + k + 3 = 0
⇒ (k + 1) (k + 3) = 0
⇒ k = −1, −3
Thus, the value of k is −1 and −3.
For k = −1:
Length of AP `= sqrt((2-(-2))^2+(2-1(-1))^2)=sqrt(4^2+3^2)=sqrt(16+9)=sqrt25=5`
For k = −3:
Length of AP `=sqrt((2-(-2))^2+(2-1(-3))^2)=sqrt(4^2+5^2)=sqrt(16+25)=sqrt41`
Thus, the length of AP is either `5 " units"` or `sqrt41 "units". `
संबंधित प्रश्न
If the point (x, y) is equidistant from the points (a + b, b – a) and (a – b, a + b), prove that bx = ay
Show that the points (1, – 1), (5, 2) and (9, 5) are collinear.
Show that four points (0, – 1), (6, 7), (–2, 3) and (8, 3) are the vertices of a rectangle. Also, find its area
The length of a line segment is of 10 units and the coordinates of one end-point are (2, -3). If the abscissa of the other end is 10, find the ordinate of the other end.
Find the distance between the following pairs of point in the coordinate plane :
(13 , 7) and (4 , -5)
Prove that the points (1 ,1),(-4 , 4) and (4 , 6) are the certices of an isosceles triangle.
Find distance between points O(0, 0) and B(– 5, 12)
Show that the point (11, – 2) is equidistant from (4, – 3) and (6, 3)
The points (– 4, 0), (4, 0), (0, 3) are the vertices of a ______.
Read the following passage:
|
Alia and Shagun are friends living on the same street in Patel Nagar. Shagun's house is at the intersection of one street with another street on which there is a library. They both study in the same school and that is not far from Shagun's house. Suppose the school is situated at the point O, i.e., the origin, Alia's house is at A. Shagun's house is at B and library is at C. |
Based on the above information, answer the following questions.
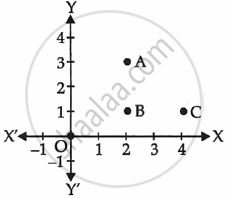
- How far is Alia's house from Shagun's house?
- How far is the library from Shagun's house?
- Show that for Shagun, school is farther compared to Alia's house and library.
OR
Show that Alia’s house, shagun’s house and library for an isosceles right triangle.
