Advertisements
Advertisements
प्रश्न
If ΔPQR and ΔSOR are both isosceles triangle on a common base OR such that P and S lie on the same side of QR. Are triangles PSQ and PSR congruent? Which condition do you use?
उत्तर
Let ∆PQR and ∆SOR are the given triangles such that PQ = PR and SQ = SR.

Now, in ∆PSQ and ∆PSR,
PQ = PR ......(Given)
SQ = SR ......(Given)
PS = PS ......(Common)
∴ ∆PSQ ≅ ∆PSR ......(SSS criterion)
Yes, the ∆PSQ and ∆PSR are congruent by using SSS criterion
APPEARS IN
संबंधित प्रश्न
In Fig, AD = CD and AB = CB.
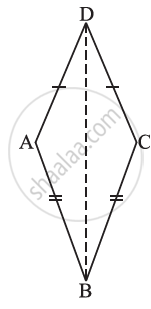
(i) State the three pairs of equal parts in ∆ABD and ∆CBD.
(ii) Is ∆ABD ≅ ∆CBD? Why or why not?
(iii) Does BD bisect ∠ABC? Give reasons.
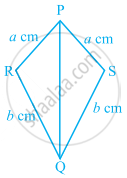
Consider the given pairs of triangles and say whether each pair is that of congruent triangles. If the triangles are congruent, say ‘how’; if they are not congruent say ‘why’ and also say if a small modification would make them congruent: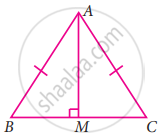
In the given figure FG = FI and H is midpoint of GI, prove that ∆FGH ≅ ∆FHI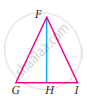
By which congruency criterion, the two triangles in the given figure are congruent?
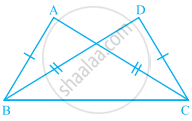
If ∆ABC and ∆DBC are on the same base BC, AB = DC and AC = DB (see figure), then which of the following gives a congruence relationship?
In ∆ABC, AB = 3.5 cm, AC = 5 cm, BC = 6 cm and in ∆PQR, PR = 3.5 cm, PQ = 5 cm, RQ = 6 cm. Then ∆ABC ≅ ∆PQR.
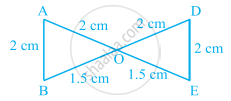
In the following pairs of triangles of figure, the lengths of the sides are indicated along the sides. By applying SSS congruence criterion, determine which triangles are congruent. If congruent, write the results in symbolic form.
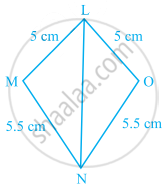
In the following pairs of triangles of figure, the lengths of the sides are indicated along the sides. By applying SSS congruence criterion, determine which triangles are congruent. If congruent, write the results in symbolic form.
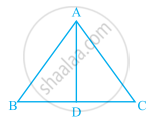
ABC is an isosceles triangle with AB = AC and D is the mid-point of base BC (see figure).
- State three pairs of equal parts in the triangles ABD and ACD.
- Is ∆ABD ≅ ∆ACD. If so why?
Triangles DEF and LMN are both isosceles with DE = DF and LM = LN, respectively. If DE = LM and EF = MN, then, are the two triangles congruent? Which condition do you use? If ∠E = 40°, what is the measure of ∠N?
