Advertisements
Advertisements
प्रश्न
If ∆PQR and ∆XYZ are congruent under the correspondence QPR `leftrightarrow` XYZ, then QP = ______.
उत्तर
If ∆PQR and ∆XYZ are congruent under the correspondence QPR `leftrightarrow` XYZ, then QP = XY.
APPEARS IN
संबंधित प्रश्न
Classify the given triangle based on its sides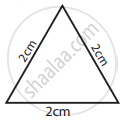
Classify the following triangle based on its sides and angles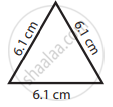
I am a closed figure with each of my three angles is 60°. Who am I?
The given triangle is _________
An equilateral triangle is
If for ∆ABC and ∆DEF, the correspondence CAB `leftrightarrow` EDF gives a congruence, then which of the following is not true?
If ∆PQR and ∆XYZ are congruent under the correspondence QPR `leftrightarrow` XYZ, then ∠R = ______.
If ∆PQR and ∆XYZ are congruent under the correspondence QPR `leftrightarrow` XYZ, then QR = ______.
If ∆PQR and ∆XYZ are congruent under the correspondence QPR `leftrightarrow` XYZ, then ∠P = ______.
If ∆PQR and ∆XYZ are congruent under the correspondence QPR `leftrightarrow` XYZ, then ∠Q = ______.
If ∆PQR and ∆XYZ are congruent under the correspondence QPR `leftrightarrow` XYZ, then RP = ______.
It is possible to have a right-angled equilateral triangle.
If M is the mid-point of a line segment AB, then we can say that AM and MB are congruent.
If the areas of two squares is same, they are congruent.
If two sides and one angle of a triangle are equal to the two sides and angle of another triangle, then the two triangles are congruent.
If two angles and a side of a triangle are equal to two angles and a side of another triangle, then the triangles are congruent.
