Question

If the line `y - sqrt(3)x + 3` = 0 cuts the parabola y² = x + 2 at A and B, then PA. PB is equal to `("where coordinates of P are" (sqrt(3), 0))` ______.

पर्याय

• `(4(sqrt(3) + 2))/3`

• `(4(2 - sqrt(3)))/3`

• `2sqrt(3)`

• `(2(sqrt(3) + 2))/3`

Answer 1

If the line `y - sqrt(3)x + 3` = 0 cuts the parabola y² = x + 2 at A and B, then PA. PB is equal to (where co-ordinates of Pare `(sqrt(3), 0)`) `underlinebb((4(sqrt(3) + 2))/3)`.

Explanation:

Given parabola is y² = x + 2 and given line is y = `sqrt(3)x - 3` and co-ordinates of P are `(sqrt(3), 0)`.

 

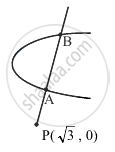
AB makes an angle of 60° with the positive direction of the x-axis. Co-ordinates of any point on this line may be taken as `(sqrt(3) + rcos 60^circ, 0 + rsin 60^circ)`

or `(sqrt(3) + r/2, (rsqrt(3))/2)`

If this point lies on y² = x + 2 then.

`3/4r^2 = sqrt(3) + r/2 + 2`

or 3r² = `4sqrt(3) + 2r + 8`

or `3r^2 - 2r - 4(2 + sqrt(3))` = 0   ...(i)

 Let r₁ and r₂ be the roots of equation (i),

Then r₁r₂ = `-(4(2 + sqrt(3)))/3`

Now PA.PB = |r₁||r₂|

= |r₁r₂|

= `4/3(2 + sqrt(3))`