Advertisements
Advertisements
प्रश्न
If x : a = y : b, prove that `(x^4 + a^4)/(x^3 + a^3) + (y^4 + b^4)/(y^3 + b^3) = ((x + y)^4 + (a + b)^4)/((x+ y)^3 + (a + b)^3`
उत्तर
`x/a = y/b` = k (say)
x = ak, y = bk
L.H.S. = `(x^4 + a^4)/(x^3 + a^3) + (y^4 + b^4)/(y^3 + b^3)`
= `(a^4k^4 + a^4)/(a^3k^3 + a^3) + (b^4k^4 + b^4)/(b^3k^3 + b^3)`
= `(a^4(k^4 + 1))/(a^3(k^3 + 1)) + (b^4(k^4 + 1))/(b^3(k^3 + 1)`
= `(a(k^4 + 1))/(k^3 + 1) + (b(k^4 + 1))/(k^3 + 1)`
= `(a(k^4 + 1) + b(k^4 + 1))/(k^3 + 1)`
= `((k^4 + 1)(a + b))/(k^3 + 1)`
R.H.S. = `((x + y)^4 + (a + b)^4)/((x+ y)^3 + (a + b)^3`
= `((ak + bk)^4 + (a + b)^4)/((ak + bk)^3 + (a + b)^3`
= `(k^4(a + b)^4 + (a - b)^4)/(k^3(a + b)^3(a + b)^3`
= `((a + b)^4(k^4 + 1))/((a + b)^3(k^3 + 1)`
= `((a + b)(k^4 + 1))/(k^3 + 1)`
= `((k^4 + 1)(a + b))/(k^3 + 1)`
∴ L.H.S. = R.H.S.
Hence proved.
APPEARS IN
संबंधित प्रश्न
In a mixture of 126 kg of milk and water, milk and water are in ratio 5 : 2. How much water must be added to the mixture to make this ratio 3 : 2?
Find the triplicate ratio of the following :
`2 sqrt 5 : 5 sqrt 2`
The sides of a triangle are in the ratio 3 : 2 : 4. If the perimeter of the triangle is 27 cm, find the length of each side.
If `(2"y"+5"x")/(3"y"-5"x")=2 1/2`, find x, if y = 70
The costs of the two articles are in the ratio 7 : 4. If the cost of the first article is Rs. 2,800; find the cost of the second article.
The income of a man is increased in the ratio of 10 : 11. If the increase in his income is Rs 600 per month, find his new income.
Find the simplified form of the following ratio.
7 : 15
A line segment 56 cm long is to be divided into two parts in the ratio of 2:5. Find the length of each part.
When Chinmay visted chowpati at Mumbai on a holiday, he observed that the ratio of North Indian food stalls to South Indian food stalls is 5:4. If the total number of food stalls is 117, find the number of each type of food stalls.
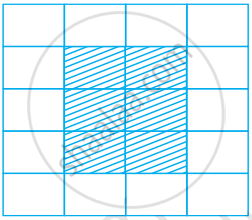
In a floral design made from tiles dimensions 40 cm by 60 cm (See figure), find the ratios of the area of the shaded portion to the area of the unshaded portion.