Advertisements
Advertisements
प्रश्न
In a colony, 275 families buy Tamil newspaper, 150 families buy English newspaper, 45 families buy Hindi newspaper, 125 families buy Tamil and English newspaper, 17 families buy English and Hindi newspapers, 5 families buy Tamil and Hindi newspaper and 3 families buy all the three newspaper. If each family buy atleast one of these newspaper then find Total number of families in the colony
उत्तर
Let T, E and H represent families buying Tamil newspaper, English newspaper and Hindi newspaper respectively.
n(T) = 275, n(E) = 150, n(H) = 45
n(T ∩ E) = 125, n(E ∩ H) = 17, n(T ∩ H) = 5
n(T ∩ E ∩ H) = 3
Let us represent the given data in Venn diagrams.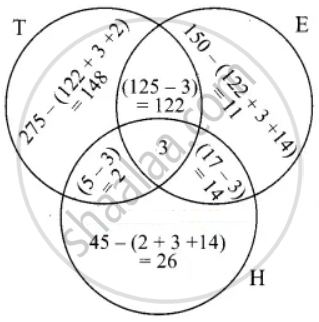
Total number of families in the colony
= 148 + 122 + 11 + 14 + 3 + 2 + 26
= 326
APPEARS IN
संबंधित प्रश्न
State, whether the pair of sets, given below, are equal sets or equivalent sets:
{8, 6, 10, 12} and {3, 2, 4, 6}
Write the cardinal number of the following set:
A = {0, 1, 2, 4}
Write the cardinal number of the following set:
E = {16, 17, 18 19}
Given:
A = {Natural numbers less than 10}
B = {Letters of the word ‘PUPPET’}
C = {Squares of first four whole numbers}
D = {Odd numbers divisible by 2}.
Find: n(B)
State true or false for the following. Correct the wrong statement.
If A = {0}, then n(A) = 0
State true or false for the following. Correct the wrong statement.
If T ={a, l, a, h, b, d, h), then n(T) = 5
If n(A) = 25, n(B) = 40, n(A ∪ B) = 50 and n(B’) = 25, find n(A ∩ B) and n(U).
Verify n(A ∪ B ∪ C) = n(A) + n(B) + n(C) – n(A ∩ B) – n(B ∩ C) – n(A ∩ C) + n(A ∩ B ∩ C) for the following sets
A = {1, 3, 5}, B = {2, 3, 5, 6}, C = {1, 5, 6, 7}
A survey of 1000 farmers found that 600 grew paddy, 350 grew ragi, 280 grew corn, 120 grew paddy and ragi, 100 grew ragi and corn, 80 grew paddy and corn. If each farmer grew atleast anyone of the above three, then find the number of farmers who grew all the three.
In a class of 50 students, each one come to school by bus or by bicycle or on foot. 25 by bus, 20 by bicycle, 30 on foot and 10 students by all the three. Now how many students come to school exactly by two modes of transport?
