Advertisements
Advertisements
प्रश्न
In a Faraday disc dynamo, a metal disc of radius R rotates with an angular velocity ω about an axis perpendicular to the plane of the disc and passing through its center. The disc is placed in a magnetic field B acting perpendicular to the plane of the disc. Determine the induced emf between the rim and the axis of the disc.
उत्तर
Assume a thin conducting disc with radius R is rotated anticlockwise around its axis in a plane perpendicular to a uniform magnetic field of induction `vec "B"` (see the figure in the above Note for reference). The arrow `vec"B"` points downward. Let the constant angular speed of the disc be ω.
Consider an infinitesimal element with radial thickness dr at r from the rotation axis. The area traced by the element in one rotation is dA = 2πrdr. Therefore, the time rate at which the element traces out the area is
`"dA"/"dt"` = frequency of rotation x dA = fdA
where f = `omega/(2pi)` is the frequency of rotation.
∴ `"dA"/"dt" = omega/(2pi) (2pi"rdr") = omega"rdr"`
The total emf induced between the axle and the rim of the rotating disc is
`|"e"| = int "B" "dA"/"dt"`
`= int_0^"R" "B"omega"rdr"`
`= "B"omega int_0^"R" "rdr"`
`= "B"omega "R"^2/2`
`= 1/2 ("B" omega"R"^2)`
For anticlockwise rotation in `vec"B"` pointing down, the axle is at a higher potential.
संबंधित प्रश्न
A horizontal wire 20 m long extending from east to west is falling with a velocity of 10 m/s normal to the Earth’s magnetic field of 0.5 × 10−4 T. What is the value of induced emf in the wire?
A stiff semi-circular wire of radius R is rotated in a uniform magnetic field B about an axis passing through its ends. If the frequency of rotation of wire is f, calculate the amplitude of alternating emf induced in the wire.
A search coil having 2000 turns with area 1.5 cm2 is placed in a magnetic field of 0.60 T. The coil is moved rapidly out of the field in a time of 0.2 s. Calculate the induced emf in the search coil.
Calculate the induced emf between the ends of an axle of a railway carriage 1.75 m long traveling on level ground with a uniform velocity of 50 kmph. The vertical component of Earth's magnetic field (Bv) is 5 × 10-5 T.
In the expression e = –dΦ/dt, the -ve sign signifies ______
A magnet is moved towards a coil (i) quickly (ii) slowly, then the induced e.m.f. is ______
The magnetic flux through a loop varies according to the relation Φ = 8t2 + 6t + 2, Φ is in milliweber and t is in second. What is the magnitude of the induced emf in the loop at t = 2 seconds?
Determine the motional emf induced in a straight conductor moving in a uniform magnetic field with constant velocity on the basis of Lorentz force.
Two coils have a mutual inductance of 0.01 H. The current in the first coil changes according to equation, I = 5 sin 200 πt. The maximum value of emf induced in the second coil is ________.
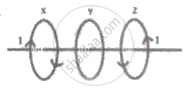
Three identical coils X, Y and Z are placed with their planes parallel to each other. Coils X and Z carry current as shown in the figure. Coils X and Y are fixed and coil Z is moved towards Y, then ______.
The area of a coil is 'A'. The coil is placed in a magnetic field which changes from 'B0' to 4B0' in time 't'. The magnitude of induced e.m.f. in the coil will be ____________.
Derive an expression for the emf induced in a straight conductor moving in a uniform magnetic field with constant velocity.
With the help of a neat labelled diagram, obtain an expression for the induced emf in a stationary coil in a changing magnetic field.
