Question

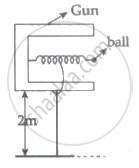
In a spring gun having spring constant 100 N/m a small ball 'B' of mass 100 g is put in its barrel (as shown in figure) by compressing the spring through 0.05 m. There should be a box placed at a distance 'd' on the ground so that the ball falls in it. If the ball leaves the gun horizontally at a height of 2 m above the ground. The value of d is ______ m.

(g = 10 m/s²).

पर्याय

• 2

• 1

• 4

• 3

Answer 1

In a spring gun having spring constant 100 N/m a small ball 'B' of mass 100 g is put in its barrel (as shown in figure) by compressing the spring through 0.05 m. There should be a box placed at a distance 'd' on the ground so that the ball falls in it. If the ball leaves the gun horizontally at a height of 2 m above the ground. The value of d is 1 m.

Explanation:

Spring constant (k) = 100 N/m

mass of a ball = 100 g = 100 × 10^-3 kg

Δx = 0.05m

Potential energy in the spring = `1/2kΔx^2`

Using the principle of energy conservation,

`1/2kDeltax^2 = 1/2mv^2`

`v = Deltaxsqrt(k/m)`

= `0.05sqrt((100)/(100 xx 10^-3))`

= 0.5`sqrt(10)` m/s

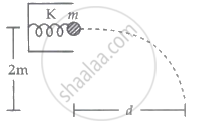
Height = (2m)

From 2^nd equation of motion,

`h = 1/2 g t^2`

or, `t = sqrt((2h)/g) = sqrt((2 xx 2)/10) = 2/sqrt(10)`

Now, `d = vt = [0.5sqrt10][2/sqrt10]` = 1m.