Advertisements
Advertisements
प्रश्न
In Δ ABC, the perpendicular from vertices A and B on their opposite sides meet (when produced) the circumcircle of the triangle at points D and E respectively. Prove that: arc CD = arc CE
उत्तर
Given: In ΔABC, the perpendiculars from vertices A and B on their opposite sides meet (when produced) the circumcircle of the triangle at points D and E respectively.
To prove: Arc CD = Arc CE
Construction: Join CE and CD
Proof :
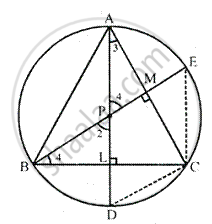
In ΔAPM and ∠BPL
∠AMP = ∠BLP [each = 90°]
∠1 = ∠2 [vertically opposite angles]
ΔAPM ~ ΔBPL [AA postulate]
∴ Third angle = Third angle
∴ ∠3 = ∠4
∴ Arc which subtends equal angle at the
Circumference of the circle are also equal.
∴ Arc CD = Arc CE
shaalaa.com
या प्रश्नात किंवा उत्तरात काही त्रुटी आहे का?
