Question

In an equilateral triangle ABC; points P, Q and R are taken on the sides AB, BC and CA respectively such that AP = BQ = CR. Prove that triangle PQR is equilateral.

Answer 1

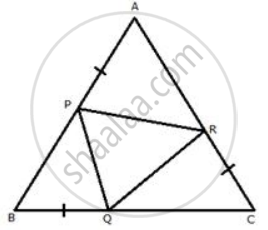
AB = BC = CA .......(i) [Given]
AP = BQ = CR .......(ii) [Given]
Subtracting (ii) from (i)
AB − AP = BC − BQ = CA − CR
BP = CQ = AR .......…(iii)
∴ ∠A = ∠B = ∠C .......(iv) [angles opp. to equal sides are equal]

In ΔBPQ and ΔCQR,
BP = CQ ........[From (iii)]
∠B = ∠C .....[From (iv)]
BQ = CR .......[Given]
∴ ΔBPQ ≅ ΔCQR .......[SAS criterion] 
⇒ PQ = QR ........(v)

In ΔCQR and ΔAPR,
CQ = AR .......[From (iii)]
∠C = ∠A ......[From (iv)]
CR = AP .......[Given]
∴ ΔCQR ≅ ΔAPR ...[SAS criterion] 
⇒ QR = PR ...(vi)

From (v) and (vi)
PQ = QR = PR
Therefore, PQR is an equilateral triangle.