Advertisements
Advertisements
प्रश्न
In Fig. 10.40, it is given that RT = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that ΔRBT ≅ ΔSAT.
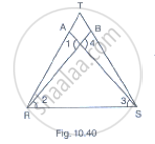
उत्तर
In the figure given that
RT=TS .......................(1)
∠=2 ∠2 ........................(2)
And `∠4=2sqrt3` ......................(3)
And given to prove ΔRBT ≅ ΔSAT
Let the point of intersection of RB and SA be denoted by O
Since RB and SA intersect at O.
∴∠AOR=∠BOS [Vertically opposite angles]
⇒ ∠1=∠4
⇒2∠2=2∠3 [From (2) and (3)]
⇒ ∠2=∠3 ......................(4)
Now we have RT= TS in ΔTRS
⇒ΔTRS is an isosceles triangle
∴∠TRS=∠TSR ............................(5) [Angles opposite to equal sides are equal]
But we have
∠TRS=∠TRB+∠2 ....................(6)
And ∠TSR=∠TSR+∠3 .....................(7)
Putting (6) and (7) in (5) we get
∠TRB+∠2=∠TSA+∠B
⇒ ∠TRB=∠TSA [∵ from (4)]
Now consider ΔRBT and ΔSAT
RT =ST [From (1)]
∠TRB=∠TSA [From (4)]
∠RTB=∠STA [Common angle]
From ASA criterion of congruence, we have ΔRBT≅ΔSAT
