Advertisements
Advertisements
प्रश्न
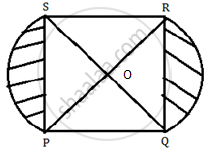
In the figure given below, PQRS is square lawn with side PQ = 42 metres. Two circular flower beds are there on the sides PS and QR with centre at O, the intersections of its
diagonals. Find the total area of the two flower beds (shaded parts).
उत्तर
Area of the square lawn PQRS = 42 m x 42 m
Let OP = OS = xm
So, x2 + x2 = (42)2
⇒ 2x2 = 42 × 42
⇒ x2 = 21 × 42
Now,
area of sector POS =
`90/360 xx pi"x"^2 = 1/4 x (pi "x"^2)` ......(i)
`= 1/4 xx 22/7 xx 21 xx 42 "m"^2` .........(ii)
Also,
Area of Δ POS = `1/4 xx "Area of square lawn PQRS"`
`= 1/4 xx (42 xx 42)^2 "m"^2` (∠POQ = 90°) ...(iii)
So,
Area of flower bed PSP = Area of sector POS - Area of Δ POS
`= 1/4 xx 22/7 xx 21 xx 42 - 1/4 xx 42 xx 42` [from (ii) and (iii)]
`= 1/4 xx 21 xx 42 xx (22/7 - 2)`
`= 1/4 xx 21 xx 42 xx (8/7) "m"^2`
Therefore area of the two flower beds = `2 xx 1/4 xx 21 xx 42 xx (8/7)`
= 504 m2
Hence , the total area of the flower beds 504 m2 .
APPEARS IN
संबंधित प्रश्न
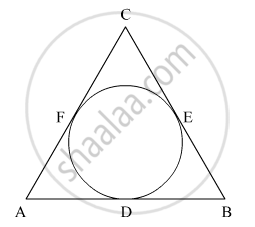
In Fig. 2, a circle is inscribed in a ΔABC, such that it touches the sides AB, BC and CA at points D, E and F respectively. If the lengths of sides AB, BC and CA and 12 cm, 8 cm and 10 cm respectively, find the lengths of AD, BE and CF.
The side of a square is 10 cm. find the area of circumscribed and inscribed circles.
Find the circumferences of a circle whose radius is 7 cm.
The radius of a sector of a circle is 7 cm. If the measure of the arc of the sector is 210°, find the area of the sector in case.
The side of a square is 10 cm. Find the area of the inscribed circle [π = 3.14]
The wheels of the locomotive of a train are 2.1 m in radius. They make 75 revolutions in one minute.
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. The length of the arc is
A wheel has a diameter of 84 cm. Find how many completer revolutions must it make to cover 3.168 km.
The cost of decorating the circumference of a circular lawn of a house at the rate of ₹ 55 per metre is ₹ 16940. What is the radius of the lawn?
In reference to a circle the value of π is equal to ______.
