Question

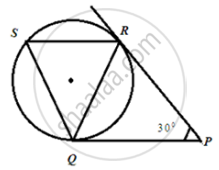
In the following figure, tangents PQ and PR are drawn to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ, then ∠RQS.

 

पर्याय

• 30°

• 60°

• 90°

• 120°

Answer 1

30°

Explanation: 

Since PQ = PR

(Lengths of tangents from the same external point are equal)

Therefore,

∠PQR = ∠QRP

Therefore in ΔPQR, we have,

∠PQR + ∠QRP + ∠QPR = 180°

2∠PQR + 30° = 180°

∠PQR = 75°

Now SR || QP

So, ∠SRQ = ∠RQP = 75° (Alternate angles)

According to the Alternate Segment Theorem which states that the angle between chord and tangent is equal to the angle in the alternate segment, we have:

∠PQR = ∠QSR = 75°

∠Q + ∠R + ∠S = 180°

∠Q = 180° - (75° + 75°)

∠Q = 30°