Advertisements
Advertisements
प्रश्न
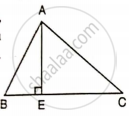
In the given figure, ∠B = 60°, AB = 16 cm and BC = 23 cm,
Calculate:
- BE
- AC
उत्तर
In ΔABE,
sin 60° = `"AE"/"AB"`
⇒ `sqrt(3)/(2) = "AE"/(16)`
⇒ AE = `sqrt(3)/(2) xx 16`
= `8sqrt(3) "cm"`
(i) In ∆ABE,
m∠AEB = 90°
∴ By Pythagoras Theorem, we get
BE2 = AB2 - AE2
⇒ BE2 = (16)2 - (8√3)2
⇒ BE2 = 256 - 192
⇒ BE2 = 64
⇒ BE = 8 cm
(ii) EC = BC - BE = 23 - 8 = 15
In ∆AEC,
m∠AEC = 90°
∴ By Pythagoras Theorem, we get
AC2 = AE2 + EC2
⇒ AC2 = (8√3)2 + (15)2
⇒ AC2 = 192 + 225
⇒ AC2 = 417
⇒ AC = 20. 42 cm
APPEARS IN
संबंधित प्रश्न
Find 'x', if :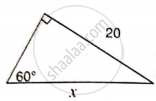
Find angle 'A' if :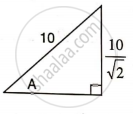
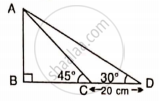
Find AD, if :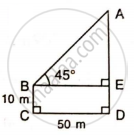
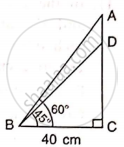
Find the length of AD.
Given: ∠ABC = 60o.
∠DBC = 45o
and BC = 40 cm.
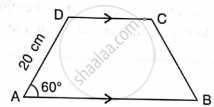
In trapezium ABCD, as shown, AB // DC, AD = DC = BC = 20 cm and ∠ A = 60°. Find: length of AB
In the given figure, AB and EC are parallel to each other. Sides AD and BC are 2 cm each and are perpendicular to AB.
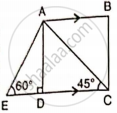
Given that ∠ AED = 60° and ∠ ACD = 45°. Calculate: AB.
In the given figure, AB and EC are parallel to each other. Sides AD and BC are 2 cm each and are perpendicular to AB.

Given that ∠ AED = 60° and ∠ ACD = 45°. Calculate: AE.
Find: AD
In right-angled triangle ABC; ∠ B = 90°. Find the magnitude of angle A, if: AB is √3 times of BC.
Find AB and BC, if: