Advertisements
Advertisements
प्रश्न
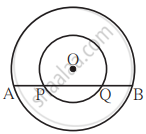
In the given figure, centre of two circles is O. Chord AB of bigger circle intersects the smaller circle in points P and Q. Show that AP = BQ.
उत्तर
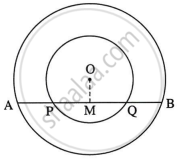
Given: Two concentric circles having centre O.
To prove: AP = BQ
Construction: Draw the line OM ⊥ chord AB such that, A-M-B
Proof:
With respect to the small circle, seg OM ⊥ chord PQ
∴ PM = MQ ...(i) ...(The perpendicular drawn from the center of the circle to the chord bisects the chord.)
Similarly, with respect to the great circle, seg OM ⊥ chord AB
∴ AM = MB ...(ii)
AM = AP + PM ...(A-P-M) ...(iii)
MB = MQ + QB ...(M-Q-B) ...(iv)
∴ AP + PM = MQ + QB ...[from (ii), (iii) and (iv)] ...(v)
∴ AP = BQ ...[from (i) and (v)]
APPEARS IN
संबंधित प्रश्न
Distance of chord AB from the centre of a circle is 8 cm. Length of the chord AB is 12 cm. Find the diameter of the circle.
Diameter of a circle is 26 cm and length of a chord of the circle is 24 cm. Find the distance of the chord from the centre.
Radius of a circle is 34 cm and the distance of the chord from the centre is 30 cm, find the length of the chord.
Radius of a circle with centre O is 41 units. Length of a chord PQ is 80 units, find the distance of the chord from the centre of the circle.
Prove that, if a diameter of a circle bisects two chords of the circle then those two chords are parallel to each other.
Radius of a circle is 10 cm and distance of a chord from the centre is 6 cm. Hence the length of the chord is ______.
The length of the longest chord of the circle with radius 2.9 cm is ______.
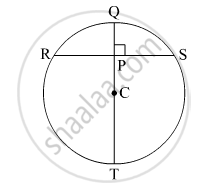
In the given figure, C is the centre of the circle. seg QT is a diameter CT = 13, CP = 5, find the length of chord RS.
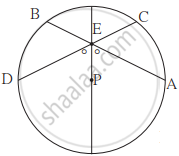
In the given figure, P is the centre of the circle. chord AB and chord CD intersect on the diameter at the point E. If ∠AEP ≅ ∠DEP then prove that AB = CD.
In the given figure, CD is a diameter of the circle with centre O. Diameter CD is perpendicular to chord AB at point E. Show that ΔABC is an isosceles triangle.

