Advertisements
Advertisements
प्रश्न
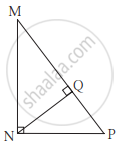
In the given figure, ∠MNP = 90°, seg NQ ⊥ seg MP, MQ = 9, QP = 4, find NQ.
बेरीज
Advertisements
उत्तर
Given: In ∆MNP,
∠MNP = 90°
NQ ⊥ MP
MQ = 9,
QP = 4
We know that.
In a right-angled triangle, the perpendicular segment to the hypotenuse from the opposite vertex is the geometric mean of the segments into which the hypotenuse is divided.
∴ NQ2 = MQ × QP ...[Theorem of geometric mean]
∴ NQ2 = 9 × 4
∴ NQ2 = 36
∴ NQ = 6 ...[Taking square root on both side]
shaalaa.com
Theorem of Geometric Mean
या प्रश्नात किंवा उत्तरात काही त्रुटी आहे का?
संबंधित प्रश्न
In the given figure, ∠QPR = 90°, seg PM ⊥ seg QR and Q–M–R, PM = 10, QM = 8, find QR.
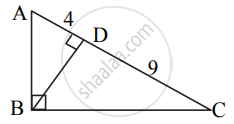
In right-angled ΔABC, BD ⊥ AC. If AD= 4, DC= 9, then find BD.
As shown figure, ∠DFE = 90°, FG ⊥ ED, if GD = 8, FG = 12, then EG = ?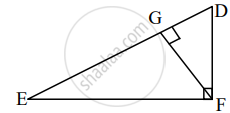
In the figure, ΔPQR is right angled at Q, seg QS ⊥ seg PR. Find x, y.
