Advertisements
Advertisements
प्रश्न
Is it possible to have a regular polygon with measure of each exterior angle as 22°?
उत्तर
The sum of all exterior angles of all polygons is 360º. Also, in a regular polygon, each exterior angle is of the same measure. Hence, if 360º is a perfect multiple of the given exterior angle, then the given polygon will be possible
Exterior angle = 22º
360º is not a perfect multiple of 22º. Hence, such polygon is not possible.
APPEARS IN
संबंधित प्रश्न
Examine the table. (Each figure is divided into triangles and the sum of the angles deduced from that.)
| Figure | 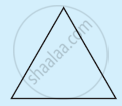 |
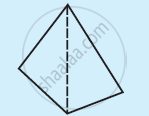 |
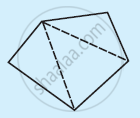 |
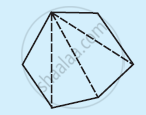 |
| Side | 3 | 4 | 5 | 6 |
| Angle sum | 180° |
2 × 180° = (4 − 2) × 180° |
3 × 180° = (5 − 2) × 180° |
4 × 180° = (6 − 2) × 180° |
What can you say about the angle sum of a convex polygon with number of sides?
a) 7
b) 8
c) 10
d) n
Find the measure of each exterior angle of a regular polygon of 9 sides.
State the name of a regular polygon of 6 sides.
What is the sum of all angles of a hexagon?
A regular polygon is a polygon whose all sides are equal and all ______ are equal.
A nonagon has ______ sides.
If the sum of interior angles is double the sum of exterior angles taken in an order of a polygon, then it is a hexagon.
A polygon is regular if all of its sides are equal.
ABCDE is a regular pentagon. The bisector of angle A meets the side CD at M. Find ∠AMC.
Find the measure of each angle of a regular octagon.
