Advertisements
Advertisements
प्रश्न
किसी बक्से मेंं 30 टिकट हैं। प्रत्येक टिकट पर 1 से 30 मेंं से एक ही संख्या लिखी गई है। इसमेंं से कोई एक टिकट यादृच्छिक पद्धति से निकाला गया तो निम्न घटनाओं की संभाव्यता ज्ञात कीजिए।
टिकट पर विषम संख्या मिलने पर।
उत्तर
मानो, बक्से में से एक टिकट यादृच्छिक पद्धति से बाहर निकालना, इस घटना का नमूना अवकाश ‘S’ है।
S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30}
∴ n(S) = 30
घटना A: टिकट पर विषम संख्या मिलने पर।
A = {1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29}
∴ n(A) = 15
∴ P(A) = `("n"("A"))/("n"("S")) = 15/30 = 1/2`
∴ P(A) = `1/2`
∴ टिकट पर विषम संख्या मिलना, इस घटना की संभाव्यता `1/2` है।
APPEARS IN
संबंधित प्रश्न
दो पाँसे एक ही समय फेंकने पर निम्नलिखित घटनाओं की संभाव्यता ज्ञात कीजिए।
पहले पाँसे के ऊपरी पृष्ठभाग पर आने वाली संख्या दूसरे पाँसे की ऊपरी पृष्ठभाग पर आने वाली संख्या से बड़ी हो।
निम्नलिखित विकल्प मेंं से कौन-सी संभाव्यता नहीं हो सकती?
1 से 100 मेंं से चुनी गई संख्या के अभाज्य संख्या होने की संभाव्यता __________ होगी।
बास्केटबॉल के खिलाड़ी जॉन, वासिम और आकाश एक निश्चित जगह बास्केटबॉल डालने का अभ्यास कर रहे थे। बास्केटबॉल डालने की जॉन की संभाव्यता `4/5`, वसिम की 0.83 तथा आकाश की 58% है। किसकी संभाव्यता अधिक है?
संयोग के खेल मेंं 1, 2, 3, 4, 5, 6, 7, 8 मेंं से किसी एक अंक पर तीर स्थिर होता है और यह समसंभाव्यता का फल है। तो निम्न घटनाओं की संभाव्यता ज्ञात कीजिए।
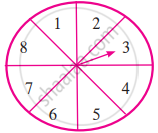
- वह तीर 8 अंक पर स्थिर होगा।
- वह तीर विषम अंक पर स्थिर होगा।
- तीर से दर्शाई गई संख्या 2 से बड़ी होगी।
- तीर से दर्शाई गई संख्या 9 से छोटी होगी।
प्रत्येक कार्डपर एक इस प्रकार से 0 से 5 यह पूर्णांक संख्याएँ लिखकर बने छह कार्ड बक्से मेंं रखे गए हैं। निम्नलिखित प्रत्येक घटनाओं की संभाव्यता ज्ञात कीजिए।
निकाले गए कार्ड की संख्या 5 से बड़ी हो।
0, 1, 2, 3, 4 इन अंकों की सहायता से दो अंकोंवाली संख्या बनानी है। अंकों की पुनरावृत्ति की जा सकती हो तो निम्न घटनाओं की संभाव्यता ज्ञात कीजिए।
वह संख्या अभाज्य संख्या होगी।
0, 1, 2, 3, 4 इन अंकों की सहायता से दो अंकोंवाली संख्या बनानी है। अंकों की पुनरावृत्ति की जा सकती हो तो निम्न घटनाओं की संभाव्यता ज्ञात कीजिए।
वह संख्या 11 की गुणज होगी।
किसी पाँसे के पृष्ठभाग पर 0, 1, 2, 3, 4, 5 यह अंक हैं। इस पाँसे को दो बार फेंकने पर ऊपरी पृष्ठभाग पर मिलने वाले अंकों का गुणनफल शून्य होने की संभाव्यता ज्ञात करें।
निम्नलिखित कृति पूर्ण कीजिए।
आपके कक्षा में विद्यार्थियों की कुल संख्या n(S) = `square`
कक्षा में चश्मा लगाने विद्यार्थियों की संख्या n(A) = `square`
सभी विद्यार्थियों में से चश्मा लगाने वाले एक विद्यार्थी के यादृच्छिक पद्धति से चुने जाने की संभाव्यता P(B) = `square`
