Advertisements
Advertisements
प्रश्न
कृती पूर्ण करा.
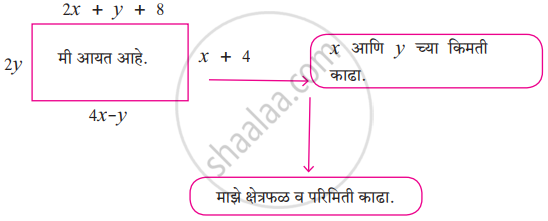
उत्तर
आयताच्या समोरासमोरील बाजू समान लांबीच्या असतात.
∴ 2x + y + 8 = 4x - y
∴ 8 = 4x - 2x - y - y
∴ 2x - 2y = 8
∴ x - y = 4 ....(i) [दोन्ही बाजूंना २ ने भागून]
तसेच, x + 4 = 2y
∴ x - 2y = - 4 ...(ii)
समीकरण (i) मधून समीकरण (ii) वजा करून,
x - y = 4
x - 2y = - 4
- + +
y = 8
y = 8 ही किंमत समीकरण (i) मध्ये ठेवून,
x - y = 4
x - 8 = 4
∴ x = 4 + 8
∴ x = 12
आता, आयताची लांबी = 4x - y
= 4(12) - 8
= 48 - 8 = 40
∴ आयताची रुंदी = 2y = 2(8) = 16
∴ आयताची परिमिती = 2 (लांबी + रुंदी)
= 2 (40 + 16)
= 2(56)
= 112 एकक
∴ आयताचे क्षेत्रफळ = लांबी × रुंदी
= 40 × 16
= 640 चौ. एकक
∴ x = 12 आणि y = 8, आयताची परिमिती 112 एकक असून आयताचे क्षेत्रफळ 640 चौ. एकक आहे.
APPEARS IN
संबंधित प्रश्न
दोन संख्यांमधील फरक ३ असून मोठ्या संख्येची तिप्पट आणि लहान संख्येची दुप्पट यांची बेरीज १९ आहे, तर त्या संख्या शोधा.
वडिलांच्या वयामध्ये मुलाच्या वयाची दुप्पट मिळवल्यास बेरीज 70 येते आणि मुलाच्या वयामध्ये वडिलांच्या वयाची दुप्पट मिळवल्यास बेरीज 95 येते, तर दोघांची वये काढा.
कांताबाईंनी दुकानातून दीड किलो चहा व पाच किलो साखर आणली. दुकानात जाऊन येण्यासाठी त्यांना 50 रुपये रिक्षाभाडे द्यावे लागले. यासाठी त्यांचे 700 रुपये खर्च झाले. नंतर त्यांना असे समजले, की या वस्तू ऑनलाइन ऑर्डर नोंदवून त्याच दराने घरपोच मिळतात. पुढील महिन्यात त्यांनी 2 किलोग्राम चहा व ७ किलोग्राम साखर ऑनलाइन मागवली, तेव्हा त्यांचा 880 रुपये खर्च झाला, तर चहा आणि साखर यांचा प्रतिकिलोग्राम दर काढा.
एका सरळ रस्त्यावर A आणि B ही दोन ठिकाणे आहेत. त्यांतील अंतर ३० किमी आहे. हमीद मोटारसायकलने A पासून B च्या दिशेने जाण्यास निघतो. त्याच वेळी जोसेफ मोटारसायकलने B पासून A च्या दिशेने जाण्यास निघतो. ते दोघे २० मिनिटांत एकमेकांना भेटतात. जोसेफ जर त्याच वेळी निघून विरुद्ध दिशेने गेला असता, तर त्याला हमीद तीन तासांनी भेटला असता, तर प्रत्येकाचा प्रवासाचा वेग किती होता?
एका आयताची लांबी त्याच्या रुंदीच्या दुपटीपेक्षा 5 ने जास्त आहे. त्या आयताची परिमिती 52 सेमी असल्यास आयताची लांबी किती?
एक व्यक्ती एका निश्चित पगार आणि दरवर्षी ठरावीक वेतनवाढ या अटींवर नोकरी सुरू करते. 4 वर्षांनी त्या व्यक्तीचा पगार रुपये 15000 आणि 10 वर्षांनी पगार रुपये 18000 असल्यास त्या व्यक्तीचा मूळ पगार आणि वेतनवाढ काढा.
समीकरण 3x - 2y = 17 मध्ये (i) y = -1 असताना x ची किंमत शोधा. (ii) x = 3 असताना y ची किंमत काढा.
एका अंकगणिती श्रेढीसाठी t17 = 54 आणि t9 = 30 असल्यास प्रथम पद (a) आणि सामान्य फरक (d) काढा.
कोणतीही दोन एकसामयिक समीकरणे लिहा- ज्यामध्ये चलांच्या किमती 12 आणि 10 असतील.
एका समद्विभुज त्रिकोणाची परिमिती 24 सेमी आहे. एकरूप बाजूंची लांबी ही पायाच्या दुपटीपेक्षा 13 सेमीने कमी आहे, तर त्या त्रिकोणाच्या सर्व बाजूंची लांबी काढा.
