Advertisements
Advertisements
प्रश्न
Length and breadth of a rectangular sheet of paper are 20 cm and 10 cm, respectively. A rectangular piece is cut from the sheet as shown in figure. Which of the following statements is correct for the remaining sheet?
पर्याय
Perimeter remains same but area changes
Area remains the same but perimeter changes
Both area and perimeter are changing
Both area and perimeter remain the same
उत्तर
Perimeter remains same but area changes
Explanation:
Perimeter of rectangular sheet = 2 × (Length + Breadth)
= 2 × (20 + 10)
= 2 × 30 = 60 cm
∴ A × Breadth = 200 cm2 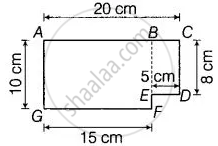
Now, perimeter of rectangular sheet after cutting the rectangular piece = Sum of all sides = 20 + 8 + 5 + 2 + 15 + 10 = 60 cm
Area = Area of rectangle ABFG + Area of rectangle BCDE = (Length × Breadth) + (Length × Breadth)
= (15 × 10) + (5 × 8)
= 150 + 40
= 190 sq cm
Hence, perimeter remains the same but area changes after cutting the piece.
APPEARS IN
संबंधित प्रश्न
Find the perimeter of a rectangle whose:
length = 10 m and breadth = 8 m
A rectangular field has length = 160m and breadth = 120 m. Find:
(i) the perimeter of the field.
(ii) the length of fence required to enclose the field.
(iii) the cost of fencing the field at the rate of? 80 per meter.
The side of a square is 3.6 cm; find its perimeter.
The perimeter of a square field is numerically equal to its area. Find each side of the square.
How much wire will be needed to make a rectangle 7 cm long and 4 cm wide?
If we take 4 rounds around a field that is 160 m long and 90 m wide, what is the distance we walk in kilometers?
The length of a rectangle is three times its breadth. If its perimeter is 64 cm, find the sides of the rectangle
Length of a rectangle is three times its breadth. Perimeter of the rectangle is 40 cm. Find its length and width.
A rectangular path of 60 m length and 3 m width is covered by square tiles of side 25 cm. How many tiles will there be in one row along its width? How many such rows will be there? Find the number of tiles used to make this path?
A large square is made by arranging a small square surrounded by four congruent rectangles as shown in the given figure. If the perimeter of each of the rectangle is 16 cm, find the area of the large square.