Question

Let 'a' be a real number such that the function f(x) = ax² + 6x – 15, x ∈ R is increasing in `(-∞, 3/4)` and decreasing in `(3/4, ∞)`. Then the function g(x) = ax² – 6x + 15, x∈R has a ______.

पर्याय

• local minimum at x = `-3/4`

• local maximum at x = `3/4`

• local minimum at x = `3/4`

• local maximum at x = `-3/4`

Answer 1

Let 'a' be a real number such that the function f(x) = ax² + 6x – 15, x ∈ R is increasing in `(-∞, 3/4)` and decreasing in `(3/4, ∞)`. Then the function g(x) = ax² – 6x + 15, x∈R has a `underlinebb("local maximum at"  x = -3/4)`.

Explanation:

f(x) = ax² + 6x – 15

∴ f'(x) = 2ax + 6

For checking monotonic behaviour

⇒ f'(x) = 0

⇒ x = `(-3)/a`

According to the question `(-3)/a = 3/4` ⇒ a = –4

Then g(x) = –4x² – 6x + 15

g'(x) = –8x – 6

For local maxima g'(x) = 0

⇒ x = `(-3)/4`

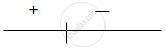sign of g'(x)

                      x = `(-3)/4`

⇒ x = `(-3)/4` is a point of local maxima.