Question

Let AB and PQ be two vertical poles, 160 m apart from each other. Let C be the middle point of B and Q, which are feet of these two poles. Let `π/8` and θ be the angles of elevation from C to P and A, respectively. If the height of pole PQ is twice the height of pole AB, then, tan² θ is equal to ______.

पर्याय

• `(3 - 2sqrt(2))/2`

• `(3 + sqrt(2))/2`

• `(3 - 2sqrt(2))/4`

• `(3 - sqrt(2))/4`

Answer 1

Let AB and PQ be two vertical poles, 160 m apart from each other. Let C be the middle point of B and Q, which are feet of these two poles. Let `π/8` and θ be the angles of elevation from C to P and A, respectively. If the height of pole PQ is twice the height of pole AB, then, tan² θ is equal to `underlinebb((3 - 2sqrt(2))/4)`.

Explanation:

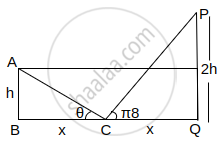
Let BC = CQ = x and AB = h and PQ = 2h

In ΔABC tan θ = `h/x`  .....(i)

In ΔPQC

`tan  π/8 = (2h)/x`  ......(ii)

Divide (i) by (ii),

`tanθ/(tan(π/8)) = 1/2`

tan θ = `1/2 tan(π/8) = 1/2(sqrt(2) - 1)`

tan² θ = `1/4(3 - 2sqrt(2))`