Advertisements
Advertisements
प्रश्न
Let f: [0, 2]→R be a twice differentiable function such that f"(x) > 0, for all x ∈( 0, 2). If `phi` (x) = f(x) + f(2 – x), then `phi` is ______.
पर्याय
increasing on (0, 2)
decreasing on (0, 2)
decreasing on (0, 1) and increasing on (1, 2)
increasing on (0, 1) and decreasing on (1, 2)
MCQ
रिकाम्या जागा भरा
उत्तर
Let f: [0, 2]→R be a twice differentiable function such that f"(x) > 0, for all x ∈( 0, 2). If `phi` (x) = f(x) + f(2 – x), then `phi` is decreasing on (0, 1) and increasing on (1, 2).
Explanation:
`phi(x)` = f(x) + f(2 – x)
`phi^'(x)` = f'(x) – f'(2 – x)
For increasing and decreasing
`phi^'(x)` = 0
⇒ `f^'(x)` = f(2 – 2)
x = 2 – x
x = 1
| Interval | (0, 1) | (1, 2) |
| sign of `phi^'(x)` | –ve | +ve |
So increasing in (1, 2) and decreasing in (0, 1)
Graph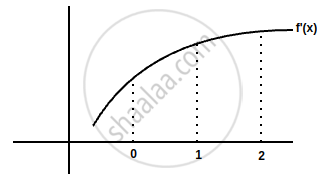
shaalaa.com
या प्रश्नात किंवा उत्तरात काही त्रुटी आहे का?
