Question

Let (h, k) be a fixed point where h > 0, k > 0. A straight line passing through this point cuts the positive direction of the coordinate axes at the points P and Q. Then the minimum area of the ΔOPQ. O being the origin, is

पर्याय

• 4hk sq.units

• 2hk sq.units

• 3hk sq.units

• None of these

Answer 1

2hk sq.units

Explanation:

Let equation of any line through the point (h, k) is `y - k = m(x - h)`  ......(i)

For this line to intersect the positive direction of two axes, m = tan θ < 0, since the angle in anticlockwise direction from x-axis becomes obtuse.

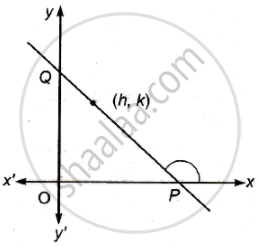
The line (i) meets x-axis in `P(h - k/m , 0)` and y-axis in `Q(0, k - mh)`.

Let A = Area of ΔOPQ

= `1/2 OP. OQ`

= `1/2(h - k/m) (k - mh)`

= `1/2 ((mh  k)/m) (k - mh)`

= `- 1/(2m) (k - mh)^2`

= `- 1/(2 tan theta) (k - h tan theta)^2`  .....`(because m = tan theta)`

= `- 1/(2 tan theta) (k^2 + h^2 tan^2theta - 2k tan theta)`

= `1/2 (2kh - k^2 cot theta - h^2 tan theta)`

⇒ `(dA)/(d theta) = 1/2 [-k^2 (- "cosec"^2theta) - h^2sec^2 theta]`

= `1/2 [k^2 "cosec"^2theta - h^2sec^2theta]`

To obtain minimum value of A, `(dA)/(d theta)` = 0

⇒ `k^2 "cose"^2 theta - h^2 sec^2 theta` = 0

⇒ `k^2/(sin^2theta) = h^2/(cos^2theta)`

⇒ `k^2/h^2 = tan^2theta`

⇒ `tan theta = +- k/h`

tan θ < 0 (given), k > 0, h > 0 (given)

Therefore, `tan theta = - k/h`  .....(Only possible value)

`(d^2A)/(d theta^2) = 1/2 [-2k^2 "cosec"^2 theta cot theta - 2h^2 sec^2 theta tan theta]`

= `-[k^2 (1 + cot^2 theta) cot theta + h^2 (1 + tan^2 theta) tan theta]`

⇒ `[(d^2A)/(d theta^2)]_(tan theta = - k/h) = -[k^2 (1 + h^2/k^2)((-h)/k) + h^2(1 + k^2/h^2)((-k)/h)]`

= `[k^2((k^2 + h^2)/k^2)(h/k) + h^2((h^2 + k^2)/h^2)(k/h)]`

= `[((k^2 + h^2)h)/k + ((h^2 + k^2)(k))/h]`

= `(k^2 + h^2)[h/k + k/h] > 0`  .....`(because h, k > 0)`

Therefore, A is least when tan θ = `- k/h`. Also, the least value of A is

A = `1/2[2hk - k^2 ((-h)/k) - h^2((-k)/h)]`

= `1/2[2hk + kh + kh]`

= 2hk