Advertisements
Advertisements
प्रश्न
Locate `sqrt(5), sqrt(10)` and `sqrt(17)` on the number line.
उत्तर
`sqrt(5)` on the number line:
5 can be written as the sum of the square of two natural numbers:
i.e., 5 = 1 + 4 = 12 + 22
On the number line,
Take OA = 2 units.
Perpendicular to OA, draw BA = 1 unit.
Join OB.
Using the Pythagoras theorem,
We have, OB = `sqrt(5)`
Draw an arc with centre O and radius OB using a compass such that it intersects the number line at the point C.
Then, we get, C corresponds to `sqrt(5)`.
Or we can say that OC = `sqrt(5)`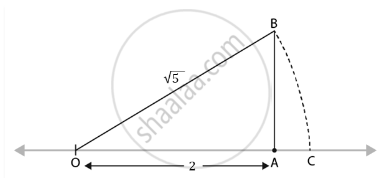
`sqrt(10)` on the number line:
10 can be written as the sum of the square of two natural numbers:
i.e., 10 = 1 + 9 = 12 + 32
On the number line,
Take OA = 3 units.
Perpendicular to OA, draw BA = 1 unit.
Join OB.
Using the Pythagoras theorem,
We have, OB = `sqrt(10)`
Draw an arc with centre O and radius OB using a compass such that it intersects the number line at the point C.
Then, the point C corresponds to `sqrt(10)`.
Or we can say that OC = `sqrt(10)`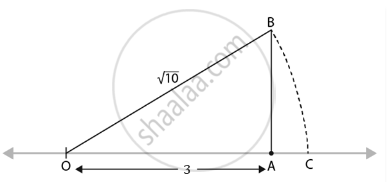
`sqrt(17)` on the number line:
17 can be written as the sum of the square of two natural numbers:
i.e., 17 = 1 + 16 = 12 + 42
On the number line,
Take OA = 4 units.
Perpendicular to OA, draw BA = 1 unit.
Join OB.
Using the Pythagoras theorem,
We have, OB = `sqrt(17)`
Draw an arc with centre O and radius OB using a compass such that it intersects the number line at the point C.
Then, point C corresponds to `sqrt(17)`.
Or, we can say that OC = `sqrt(17)`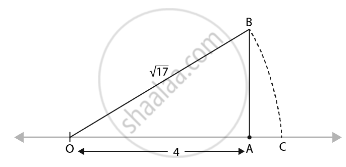
APPEARS IN
संबंधित प्रश्न
Visualise 3.765 on the number line, using successive magnification.
Visualise the representation of `5.3bar7` on the number line upto 5 decimal places, that is upto 5.37777.
The number 0.318564318564318564 ........ is:
If n is a natural number, then \[\sqrt{n}\] is
The smallest rational number by which`1/3`should be multiplied so that its decimal expansion terminates after one place of decimal, is
Represent the following numbers on the number line
5.348
Represent the following number on the number line:
7.2
Represent the following number on the number line:
`(-3)/2`
Represent geometrically the following number on the number line:
`sqrt(8.1)`
Represent geometrically the following number on the number line:
`sqrt(2.3)`
