Advertisements
Advertisements
प्रश्न
माचिस की तीलियों की सहायता से त्रिभुज बनाने का प्रयत्न कीजिए। इनमें से कुछ आकृति में दिखाए गए हैं।
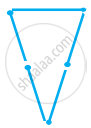 |
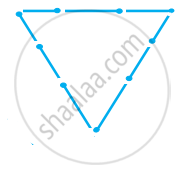 |
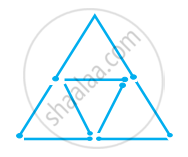 |
क्या आप 6 माचिस की तीलियों से एक त्रिभुज बना सकते हैं?
(ध्यान रखिए की आपको प्रत्येक स्थिति में सभी उपलब्ध माचिस की तीलियों का उपयोग करना है)। प्रत्येक स्थिति में त्रिभुज के प्रकार का नाम बताइए। यदि आप त्रिभुज नहीं बना पाते हैं, तो उसके कारण के बारे में सोचिए।
उत्तर
यह एक न्यूनकोण त्रिभुज है और 6 माचिस की तीलियों की सहायता से एक त्रिभुज बनाना संभव है क्योंकि इसकी दो भुजाओं का योग तीसरी भुजा से अधिक होता है।
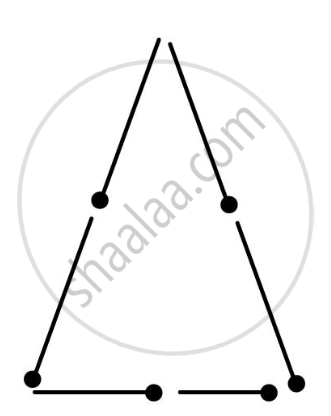
APPEARS IN
संबंधित प्रश्न
पाँच त्रिभुज खींचिए और उनकी भुजाओं को मापिए। प्रत्येक स्थिति में जाँच कीजिए कि किन्हीं दो भुजाओं की लंबाईओं का योग तीसरी भुजा की लंबाई से सदैव बड़ा है।
निम्नलिखित त्रिभुज का प्रकार लिखिए:
निम्नलिखित त्रिभुज का प्रकार लिखिए:
∆DEF जिसमें m∠D = 90° हैं।
निम्नलिखित त्रिभुज का प्रकार लिखिए:
ΔXYZ जिसमें m∠Y = 90° और XY = YZ हैं।
निम्नलिखित त्रिभुज का प्रकार लिखिए:
ΔLMN जिसमें m∠L = 30°, m∠M = 70° और m∠N = 80° हैं।
निम्न का सुमेलन कीजिए:
|
|
त्रिभुज के माप |
|
त्रिभुज का प्रकार |
|
(i) |
समान लंबाई की तीन भुजाएँ |
(a) |
विषमबाहु समकोण त्रिभुज |
|
(ii) |
समान लंबाई की दो भुजाएँ |
(b) |
समद्विबाहु समकोण त्रिभुज |
|
(iii) |
अलग-अलग लंबाईयों की सभी भुजाएँ |
(c) |
अधिक कोण त्रिभुज |
|
(iv)
|
3 न्यूनकोण
|
(d) |
समकोण त्रिभुज |
|
(v)
|
1 समकोण
|
(e) |
समबाहु त्रिभुज |
|
(vi)
|
1 अधिक कोण
|
(f) |
न्यून कोण त्रिभुज |
|
(vii) |
दो बराबर लंबाईयों की भुजाओं के साथ एक 1 समकोण |
(g) |
समद्विबाहु त्रिभुज |
निम्नलिखित त्रिभुज का दो प्रकार से नामकरण कीजिए (आप कोण का प्रकार केवल देखकर ज्ञात कर सकते हैं।)

निम्नलिखित त्रिभुज का दो प्रकार से नामकरण कीजिए (आप कोण का प्रकार केवल देखकर ज्ञात कर सकते हैं।)
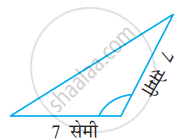
माचिस की तीलियों की सहायता से त्रिभुज बनाने का प्रयत्न कीजिए। इनमें से कुछ आकृति में दिखाए गए हैं।
 |
 |
 |
क्या आप 5 माचिस की तीलियों से एक त्रिभुज बना सकते हैं?याँ
(ध्यान रखिए की आपको प्रत्येक स्थिति में सभी उपलब्ध माचिस की तीलियों का उपयोग करना है)। प्रत्येक स्थिति में त्रिभुज के प्रकार का नाम बताइए। यदि आप त्रिभुज नहीं बना पाते हैं, तो उसके कारण के बारे में सोचिए।
एक सम षड्भुज (regular hexagon) का एक रफ़ चित्र खींचिए। उसके किसी तीन शीर्षों को जोड़कर एक त्रिभुज बनाइए। पहचानिए कि आपने किस प्रकार का त्रिभुज खींचा है।
