Advertisements
Advertisements
प्रश्न
Nathan, an engineering student was asked to make a model shaped like a cylinder with two cones attached at its two ends. The diameter of the model is 3 cm and its length is 12 cm. If each cone has a height of 2 cm, find the volume of the model that Nathan made.
उत्तर
Radius of the cone = Radius of the cylinder

r = `3/2` cm
Height of the cone (H) = 2 cm
Height of the cylinder (h) = 12 – (2 + 2) cm = 8 cm
Volume of the model = Volume of the cylinder + Volume of 2 cones
= `pi"r"^2"h" + 2 xx 1/3 pi"r"^2"H"`
= `pi"r"^2("h" + 2/3"H")"cm"^3`
= `22/7 xx 3/2 xx 3/2 (8 + 2/3 xx 2)"cm"^3`
= `(11 xx 3 xx 3)/(7 xx 2) ((24 + 4)/3)"cm"^3`
= `(11 xx 3 xx 3 xx 28)/(7 xx 2 xx 3)"cm"^3`
= `(11 xx 3 xx 4)/2 "cm"^3`
= 11 × 3 × 2 cm3
= 66 cm3
Volume of the model = 66 cm3
APPEARS IN
संबंधित प्रश्न
Water flows at the rate of 15 m per minute through a cylindrical pipe, having the diameter 20 mm. How much time will it take to fill a conical vessel of base diameter 40 cm and depth 45 cm?
The dimensions of a cuboid are 44 cm, 21 cm, 12 cm. It is melted and a cone of height 24 cm is made. Find the radius of its base.
A tin maker converts a cubical metallic box into 10 cylindrical tins. The side of the cube is 50 cm and the radius of the cylinder is 7 cm. Find the height of each cylinder so made, if the wastage of 12% is incurred in the process `(pi = 22/7)`
A vessel is in the form of a hemispherical bowl mounted by a hollow cylinder. The diameter is 14 cm and the height of the vessel is 13 cm. Find the capacity of the vessel
From a solid cylinder whose height is 2.4 cm and the diameter 1.4 cm, a cone of the same height and same diameter is carved out. Find the volume of the remaining solid to the nearest cm3.
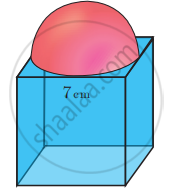
As shown in the figure a cubical block of side 7 cm is surmounted by a hemisphere. Find the surface area of the solid.
A right circular cylinder just encloses a sphere of radius r units. Calculate the ratio of the areas of the sphere and cylinder
If two solid hemispheres of same base radius r units are joined together along with their bases, then the curved surface area of this new solid is ______.
Find volume of solid generated by revolving parabola y2. = 4ax, cut of by latus rectum, about tangent at vertex.
A right circular cylinder which is open at the top and has a given surface area, will have the greatest volume if its height h and radius r are related by
