Advertisements
Advertisements
प्रश्न
निम्नलिखित आकृति में BM = BN हैं, M रेखाखंड AB का मध्य-बिंदु है तथा N रेखाखंड BC का मध्य-बिंदु है। दर्शाइए कि AB = BC है।

उत्तर
दिया गया है, BM = BN ...(i)
M, AB का मध्य-बिंदु है।
∴ AM = BM = `1/2` AB
⇒ 2AM = 2BM = AB ...(ii)
और N, BC का मध्य-बिंदु है।
∴ BN = NC = `1/2` BC
⇒ 2BN = 2NC = BC ...(iii)
यूक्लिड के सिद्धांत के अनुसार, जो चीजें एक ही चीज की दोगुनी होती हैं वे एक दूसरे के बराबर होती हैं।
समीकरण के दोनों पक्षों (i) को 2 से गुणा करने पर, हमें प्राप्त होता है।
2BM = 2BN
⇒ AB = BC ...[समीकरण (ii) और (iii) का प्रयोग करके]
APPEARS IN
संबंधित प्रश्न
निम्नलिखित कथन सत्य हैं या असत्य हैं? अपने उत्तर के लिए कारण दीजिए।
आकृति में, यदि AB = PQ और PQ = XY, तो AB = XY होगा।

निम्नलिखित पद की परिभाषा दीजिए। क्या इनके लिए कुछ ऐसे पद हैं, जिन्हें परिभाषित करने की आवश्यकता है? वे क्या हैं और आप इन्हें कैसे परिभाषित कर पाएँगे?
समांतर रेखाएँ
निम्नलिखित पद की परिभाषा दीजिए। क्या इनके लिए कुछ ऐसे पद हैं, जिन्हें परिभाषित करने की आवश्यकता है? वे क्या हैं और आप इन्हें कैसे परिभाषित कर पाएँगे?
वृत्त की त्रिज्या
नीचे दी हुई दो अभिधरणाओं पर विचार कीजिए:
- दो भिन्न बिंदु A और B दिए रहने पर, एक तीसरा बिंदु C ऐसा विद्यमान है जो A और B के बीच स्थित होता है।
- यहाँ कम से कम ऐसे तीन बिंदु विद्यमान हैं कि वे एक रेखा पर स्थित नहीं हैं।
यदि दो बिंदुओं A और B के बीच एक बिंदु C ऐसा स्थित है कि AC = BC है, C रेखाखंड AB का एक मध्य-बिंदु कहलाता है। सिद्ध कीजिए कि एक रेखाखंड का एक और केवल एक ही मध्य-बिंदु होता है।
पाइथागोरस एक विद्यार्थी था :
निम्नलिखित में से किसको उपपत्ति की आवश्यकता है?
निम्नलिखित प्रश्न को उपयुक्त यूक्लिड की अभिगृहीत का प्रयोग करते हुए, हल कीजिए :
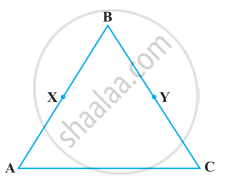
निम्नलिखित आकृति में, हमें प्राप्त है :
BX = `1/2` AB, BY = `1/2` BC तथा AB = BC है। दर्शाइए कि BX = BY है।
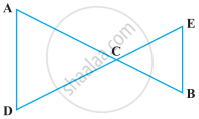
निम्नलिखित प्रश्न को उपयुक्त यूक्लिड की अभिगृहीत का प्रयोग करते हुए, हल कीजिए :
निम्नलिखित आकृति में, AC = DC और CB = CE है। दर्शाइए कि AB = DE है।
निम्नलिखित कथन का अध्ययन कीजिए :
“दो प्रतिच्छेदी रेखाएँ एक ही रेखा पर लंब नहीं हो सकती हैं।”
जाँच कीजिए कि क्या यह कथन यूक्लिड पाँचवीं अभिधारणा का समतुल्य रूपांतरण है।
[संकेत : उपरोक्त कथन में, दो प्रतिच्छेदी रेखा l और m तथा एक अन्य रेखा n की पहचान कीजिए।]
