Advertisements
Advertisements
प्रश्न
One card is drawn from a well-shuffled deck of 52 cards. Find the probability of getting the jack of hearts.
उत्तर
Total number of cards in a well-shuffled deck = 52
Total number of Jack of hearts = 1
P (getting a Jack of hearts) =`"Number of favourable outcomes"/"Total number of outcomes"`
=` 1/52`
APPEARS IN
संबंधित प्रश्न
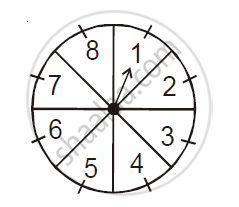
A game of chance consists of spinning an arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8 (see the given figure), and these are equally likely outcomes. What is the probability that it will point at
- 8?
- an odd number?
- a number greater than 2?
- a number less than 9?
Three coins are tossed together. Find the probability of getting no tails
What is the probability that a leap year has 53 Sundays and 53 Mondays?
A card is drawn at random from a pack of 52 cards. Find the probability that card drawn is either a black card or a king
One card is drawn from a well-shuffled deck of 52 cards. Find the probability of getting a king of red colour.
A card is drawn at random from a pack of 52 cards. Find the probability that card drawn is a heart
A bag contains 6 red, 8 black and 4 white balls. A ball is drawn at random. What is the probability that ball drawn is not black?
A bag contains 5 white and 7 red balls. One ball is drawn at random. What is the
probability that ball drawn is white?
A game consists of spinning an arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12; as shown below.
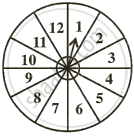
If the outcomes are equally likely, find the probability that the pointer will point at:
- 6
- an even number.
- a prime number.
- a number greater than 8.
- a number less than or equal to 9.
- a number between 3 and 11.
Three coins are tossed together. Write all the possible outcomes. Now, find the probability of getting all tails.
Find the probability that in a leap year there will be 53 Tuesdays ?
How many possibilities is following?
Select one card from the pack of 52 cards.
Two dice are thrown simultaneously. Find the probability of getting: an even number as the sum.
A child has a die whose six faces show the letters as given below:
| A | B | C | D | E | F |
The die is thrown once. The probability of getting a ‘D’ is ____________.
Two dice are numbered 1, 2, 3, 4, 5, 6 and 1, 1, 2, 2, 3, 3, respectively. They are thrown and the sum of the numbers on them is noted. Find the probability of getting each sum from 2 to 9 separately.
Complete the following table.
| Sr. No. | Random experiment | Sample space | Number of sample points in S |
| 1. | One coin is tossed. | S = {H, T} | n(S) = `square` |
| 2. | Two coins are tossed. | S = `square` | n(S) = `square` |
| 3. | Three coins are tossed. | S = {`square`, THH, HTT, THT, TTH, TTT} | n (S) = 8 |
| 4. | A die is thrown. | S = `square` | n(S) = `square` |
The table given below shows the months of birth of 36 students of a class:
| Month of birth |
Jan. | Feb. | Mar. | Apr. | May | June | July | Aug. | Sept. | Oct. | Nov. | Dec. |
| No. of students |
4 | 3 | 5 | 0 | 1 | 6 | 1 | 3 | 4 | 3 | 4 | 2 |
A student is choosen at random. Fill in the boxes.
Total number of students = `square`
Let E be the event that the selected student is born in June.
Then,
Number of times event E occurs = `square`
So, P (selected student is born in June)
P(E) = `"Number of students born in June"/square`
= `square/square`
= `square`
The percentages of marks obtained by a student in six unit tests are given below:
| Unit test | 1 | 2 | 3 | 4 | 5 | 6 |
| Percentage of marks obtained |
53 | 72 | 95 | 46 | 67 | 59 |
A unit test is selected at random. What is the probability that the student gets more than 60% marks in the test?
An unbiased die is thrown. The probability of getting an odd prime number is ______.
A bag contains 30 discs numbered from 1 to 30. One disc is drawn at random from the bag. Find the probability that it bears a number divisible by 6.
