Advertisements
Advertisements
प्रश्न
Payload is defined as the difference between the mass of displaced air and the mass of the balloon. Calculate the payload when a balloon of radius 10 m, mass 100 kg is filled with helium at 1.66 bar at 27°C. (Density of air = 1.2 kg m–3 and R = 0.083 bar dm3 K–1 mol–1).
उत्तर
Given,
Radius of the balloon, r = 10 m
∴ Volume of the balloon = `4/3pi"r"^3`
`= 4/3 xx22/7 xx 10^3`
`= 4190.5 " m"^3 ("approx")`
Thus, the volume of the displaced air is 4190.5 m3.
Given,
Density of air = 1.2 kg m–3
Then, mass of displaced air = 4190.5 × 1.2 kg
= 5028.6 kg
Now, mass of helium (m) inside the balloon is given by,
`"m" = ("MpV")/("RT")`
Here
`"M" = 4 xx 10^(-3) "kg mol"^(-1)`
p = 1.66 bar
V = Volume of the balloon
= `4190.5 " m"^3`
`"R" = 0.083 " bar" " dm"^3 "K"^(-1) "mol"^(-1)`
`"T" = 27^@"C" = 300 "K"`
Then `"m" = (4xx10^(-3)xx1.66xx4190.5xx10^3)/(0.083 xx300)`
= 1117.5 kg (approx)
Now, total mass of the balloon filled with helium = (100 + 1117.5) kg
= 1217.5 kg
Hence, pay load = (5028.6 – 1217.5) kg
= 3811.1 kg
Hence, the pay load of the balloon is 3811.1 kg.
APPEARS IN
संबंधित प्रश्न
A vessel of 120 mL capacity contains a certain amount of gas at 35 °C and 1.2 bar pressure. The gas is transferred to another vessel of volume 180 mL at 35 °C. What would be its pressure?
Using the equation of state pV = nRT; show that at a given temperature density of a gas is proportional to gas pressure p.
What will be the pressure of the gaseous mixture when 0.5 L of H2 at 0.8 bar and 2.0 L of dioxygen at 0.7 bar are introduced in a 1L vessel at 27°C?
Gases deviate from ideal behavior at high pressure. Which of the following statement(s) is correct for non-ideality?
With regard to the gaseous state of matter which of the following statements are correct?
(i) Complete order of molecules
(ii) Complete disorder of molecules
(iii) Random motion of molecules
(iv) Fixed position of molecules
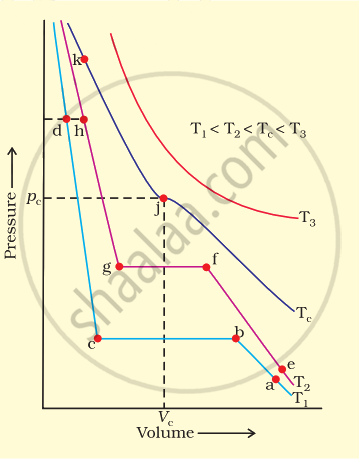
Isotherms of carbon dioxide at various temperatures are represented in figure. Answer the following questions based on this figure.
(i) In which state will \[\ce{CO2}\] exist between the points a and b at temperature T1?
(ii) At what point will \[\ce{CO2}\] start liquefying when temperature is T1?
(iii) At what point will \[\ce{CO2}\] be completely liquefied when temperature is T2.
(iv) Will condensation take place when the temperature is T3.
(v) What portion of the isotherm at T1 represent liquid and gaseous \[\ce{CO2}\] at equilibrium?