Question

Prove that the area of the triangle BCE described on one side BC of a square ABCD as base is one half the area of the similar Triangle ACF described on the diagonal AC as base

Answer 1

ABCD is a square. ∆BCE is described on side BC is similar to ∆ACF described on diagonal AC.
Since ABCD is a square. Therefore,

AB = BC = CD = DA and, AC = √2 BC [∵ Diagonal = √2 (Side)]

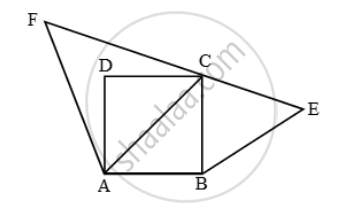
Now, ∆BCE ~ ∆ACF

`\Rightarrow \frac{Area\ (\Delta BCE)}{Area\ (\Delta ACF)}=(BC^2)/(AC^2`

`\Rightarrow \frac{Area\ (\Delta BCE)}{Area\ (\Delta ACF)}=(BC^2)/(sqrt2BC)=1/2`

`⇒ Area (∆BCE) = \frac { 1 }{ 2 } Area (∆ACF)`